赣州市网站建设_网站建设公司_Oracle_seo优化

个人主页:兜里有颗棉花糖
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创
收录于专栏【MySQL学习专栏】🎈
本专栏旨在分享学习MySQL的一点学习心得,欢迎大家在评论区讨论💌
目录
- 一、前言
- 二、导入MySQL驱动包
- 如何下载MySQL驱动包
- 如何向项目中导入MySQL驱动包
- 三、JDBC编程
- 创建数据源
- 与数据库服务器建连接
- 构造SQL语句
- 执行SQL语句
- 释放必要资源,关闭连接
- 向数据库中插入数据完整代码
- 查询数据库中的数据完整代码
- 四、JDBC编程注意事项
一、前言
JDBC编程(Java Database Connectivity)简单来说就是通过JAVA代码来操作数据库。我们在绝大部分的实际开发过程中,都是通过代码来操作数据库的(既然想用代码来操作数据库的话最主要的还是依赖我们之前学过的SQL语句)。
首先我们要知道,一个成熟的数据库一般都会提供API(Application Programming Interface,叫做应用程序编程接口)来供开发者使用,
API就是一些类/方法。API是一个非常广义的概念,这与我们之前JAVA语法中学到的Interface接口是有所区别的。
Java语法中的Interface接口特指的是Java语法中的特殊语法格式(Interface算是一个非常狭义的概念)。实际上,Java中的Interface接口也是提供API的一种方式。
通常我们写好一个程序之后,这个程序要给别人提供哪些功能,这些功能往往是通过函数/类这样的方式来提供的。
比如,我们之前Java语法阶段学过的Random、Scanner、ArrayList、String等这些都可以认为是Java标准库为我们提供的API
每个数据库提供的API都是不一样的。例如MySQL中有MySQL数据库提供的数据库、Oracle中有Oracle数据库提供的API、SQLServe数据库中有SQLServe提供的API、SQLite数据库中有SQLite数据库提供的API。
又因为设计每个数据库的人都是不一样的。所以每个数据库设计出来的API差异很大。这也会大大增加开发者的学习成本。
此时,java就提供了一套操作数据库的API,这个API存在的意义就是可以让所有的数据库都能按照统一的方式来进行操作使用数据库。所以开发者只需要学会一套API就可以操作各种数据库了。(然而这只是针对Java开发者而言)
对于C++开发者而言的话就没有这么方便了,我们已经知道每个数据库都有自己的一套API,一些比较大的公司为了让C++开发者更加方便的操作数据库也尝试开发出一套统一的API,但是开发出来的统一API也是有很多套的,导致这些不同公司或者组织开发出来的不同的统一API谁也不服谁,知道现在,也没有哪一套统一API能够向JDBC可以操作各种数据库。
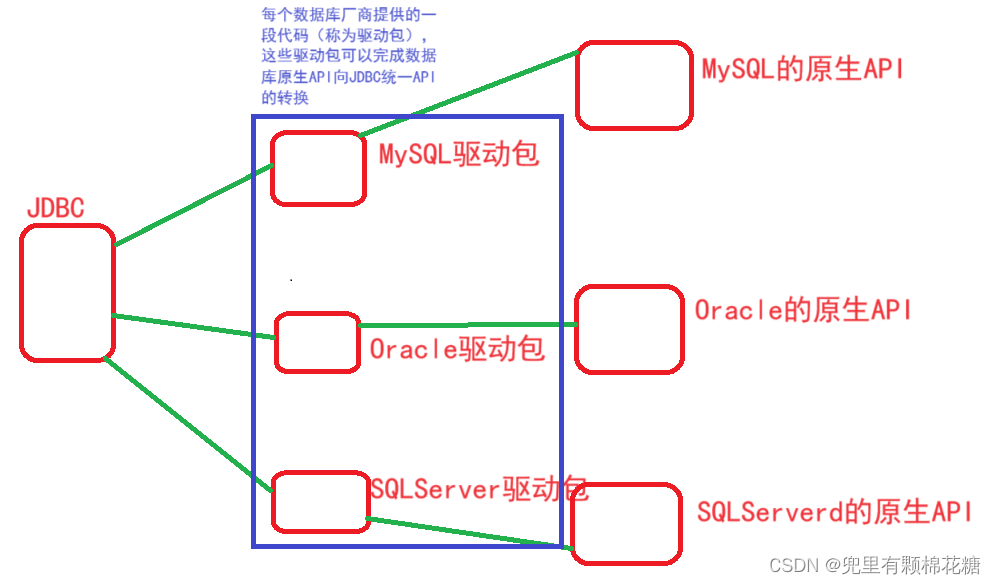
好了,现在我们把关注点放到JDBC上面,我们已经知道JDBC提供了统一的一套API来供Java开发者来操作各种数据库,但是我们不要忘记每一个数据库本身都是有自己的一套API的(JDBC只是把这些API进行统一成了一套API)。所以每个数据库厂商就提供了一些代码(
这些代码就称为数据库的驱动包)来把数据库自己的原生API转换为JDBC的统一API。请看下图方便大家理解:
二、导入MySQL驱动包
如何下载MySQL驱动包
现在我们需要引入MySQL的驱动包,来作为项目的依赖,即把MySQL驱动包下载下来导入到项目中。
关于MySQL驱动包下载的方法有很多种,我们这里采取的是从中央仓库中进行下载,中央仓库网址:https://mvnrepository.com/
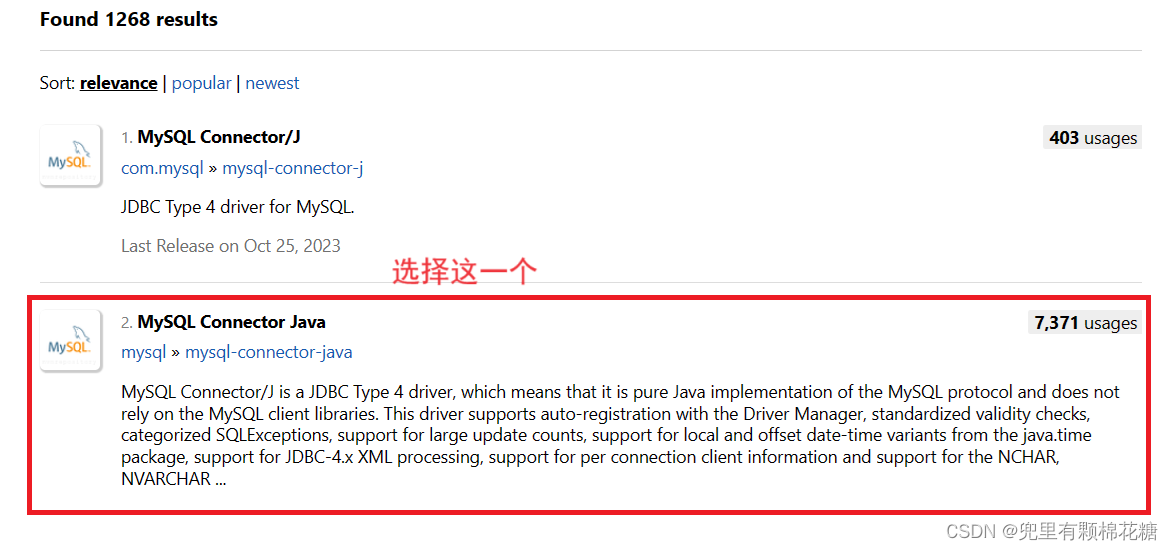
现在我们进行下载的演示:
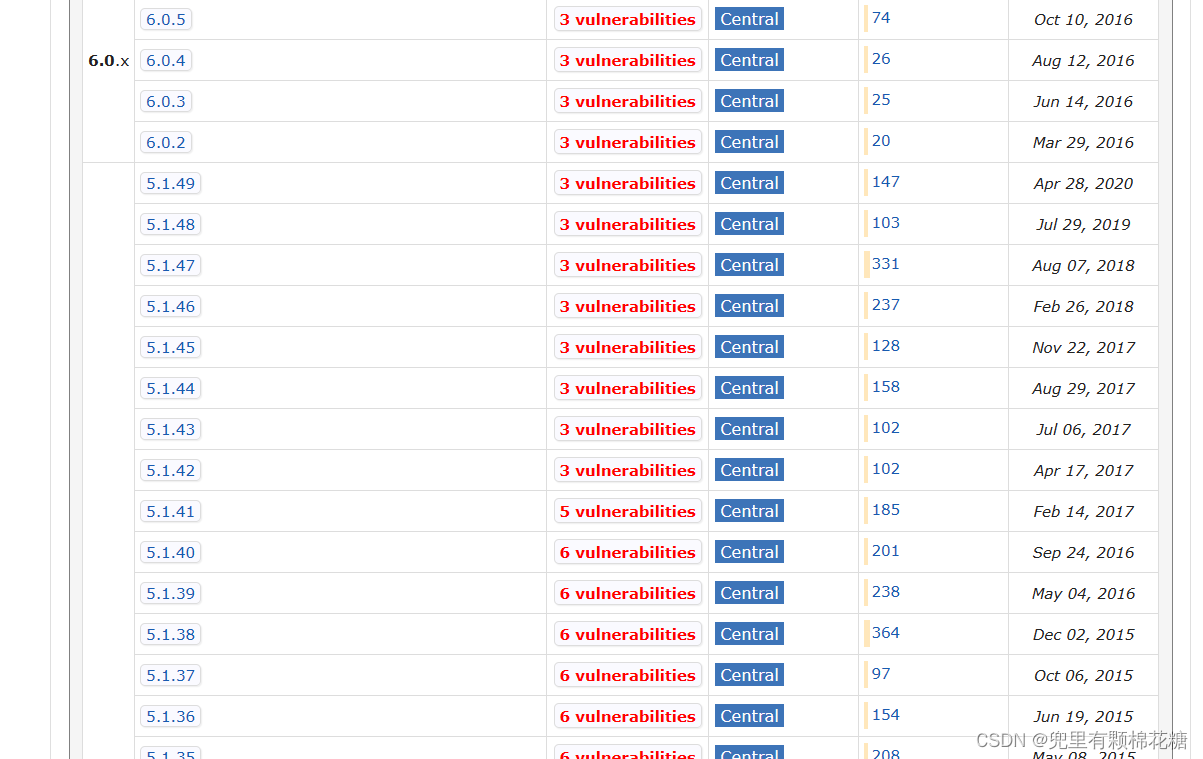
然后选择自己所需要的版本即可(数据库驱动包的版本和数据库服务器的大版本必须保持一致,小版本的话不做要求):
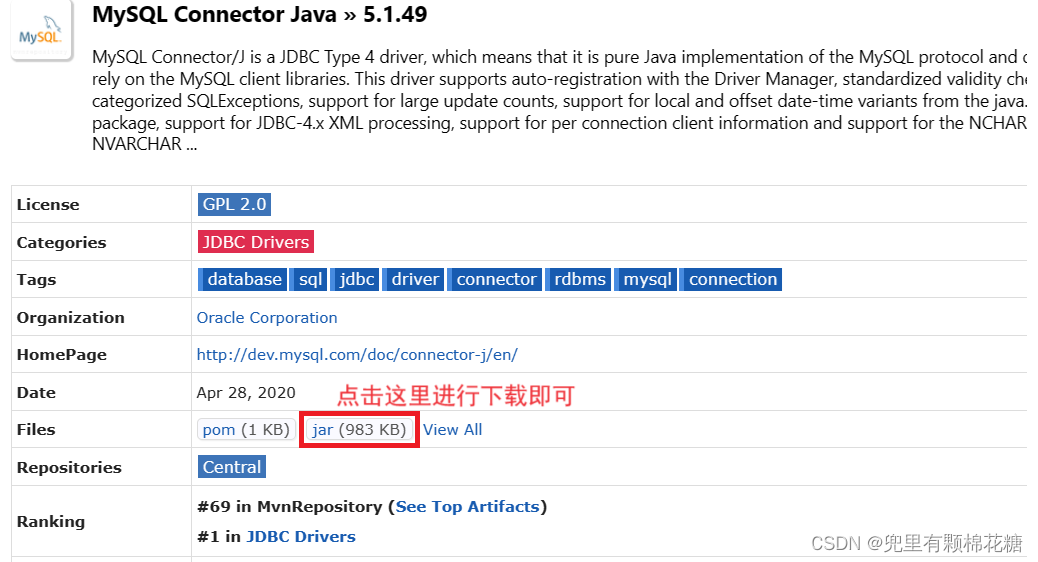
我这里下载的是5.1.49版本的:
下载成功之后大概长这个样子:
这就算是MySQL驱动包下载好了。
我们来解释一下下载的这个jar包是个什么东西:
.jar类似于是.rar这样的压缩包,是java定义的一种压缩格式,.jar包中包含了很多的.class文件。
那那么多的.class文件是干什么用的呢:一般我们要想把程序发布给其它人的话,就需要把这些.class文件拷贝过去,而如果.class文件特别多的话,就显得非常的麻烦,所以我们一般就会把这些.class文件打成压缩包的形式,即打成java定义的一种压缩格式,即.jar格式。
如何向项目中导入MySQL驱动包
现在我们已经有了MySQL驱动包,接下来我们看看如何来将其导入到我们的项目中。
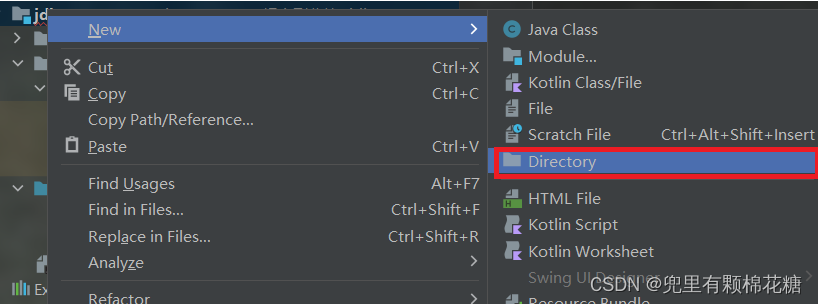
首先我们在项目中新创建一个目录,取名叫
lib(lib即library,在计算机中就是库的意思):
然后我们ctrl+c复制一下刚刚的.jar包,然后ctrl+v粘贴到lib目录中去,请看:
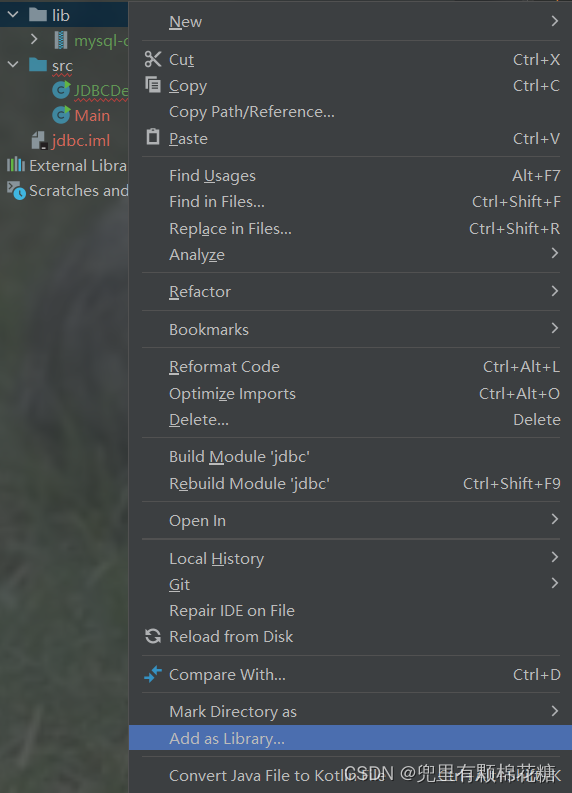
最后一步:右键lib目录,然后点击Add as Library(点击之后会弹出来一个小弹窗,我们点击OK即可),这一步意思就是告诉idea这个lib目录中放的是库文件(即.jar包)
三、JDBC编程
创建数据源
关键代码1:DataSource dataSource = new MysqlDataSource();
解释:
DataSource dataSource = new MysqlDataSource();
DataSource是JDBC提供的interface;MysqlDataSource()是MySQL驱动包提供的类,这个类就实现了JDBC提供的interface(即DataSource)。
DataSource dataSource = new MysqlDataSource();是一个向上转型(父类引用指向子类对象)的操作。
关键代码2:((MysqlDataSource) dataSource).setUrl("jdbc:mysql://127.0.0.1:3306/mysql_java?characterEncoding=utf8&useSSL=false");
解释,此代码就是向下转型,目的就是使用
setUrl()方法,这个方法是子类才有的。
好了,现在我们如果既不是用向上转型也不使用向下转型,我们就可以把关键代码1和关键代码2一起改为:
MysqlDataSource dataSource = new MysqlDataSource(); dataSource.setUrl("jdbc:mysql://127.0.0.1:3306/mysql_java?characterEncoding=utf8&useSSL=false");,这种写法(不使用转型)完全是可以的。我们之所以使用关键代码1和关键代码2这种转型的写法就是希望MysqlDataSource这个类不要扩散到代码的其它部分,即目的就是想mysql驱动包和项目代码之间的耦合关系,避免以后更换数据库的时候有太大的成本。或者当我们写的代码比较简单的时候,其实不需要太在意耦不耦合的事项,所以这两种方式在代码比较简单的时候无论用哪种方式都是可以的。我们这里使用关键代码1和关键代码2的这一种方式。
url是什么:url是唯一资源定位符,通常用来描述url来描述网络上一个资源的位置。而MySQL本体是一个服务器,相当于网络上的一个资源。
现在我们来看看setUrl()方法中
"jdbc:mysql://127.0.0.1:3306/mysql_java?characterEncoding=utf8&useSSL=false"是什么:
jdbc:mysql:jdbc:mysql意思就是给jdbc中的mysql用的。127.0.0.1是一个ip地址,相当于网路上一个设备的地址(网络上的ip地址通常是使用来进行表示的一串数字,每个部分的数值范围是1到255,用.进行分割)而127.0.0.1(环回地址)这个ip地址是一个比较特殊的ip地址,特指我们自己电脑的主机。如果我们的数据库和java代码都是在同一个主机上进行执行的,那么我们这里的ip地址就可以把ip地址写成环回ip(即127.0.0.1)。3306:3306是一个端口号,是用来区分主机上的应用程序的。比如,我的电脑上此时正在运行着许多的应用程序,即是用来区分应用程序上的进程的。characterEncoding=utf8统一字符集为utf8useSSL=false决定了数据库服务器和客户端之间的通信是否要进行加密。
设置了url之后,我们还需要设置用户名和密码。代码如下:
((MysqlDataSource) dataSource).setUser("root");
((MysqlDataSource) dataSource).setPassword("111111");
至此,我们只是找到了数据库服务器的地址,并没有连接上数据库服务器。
与数据库服务器建连接
现在,我们来尝试连接数据库。
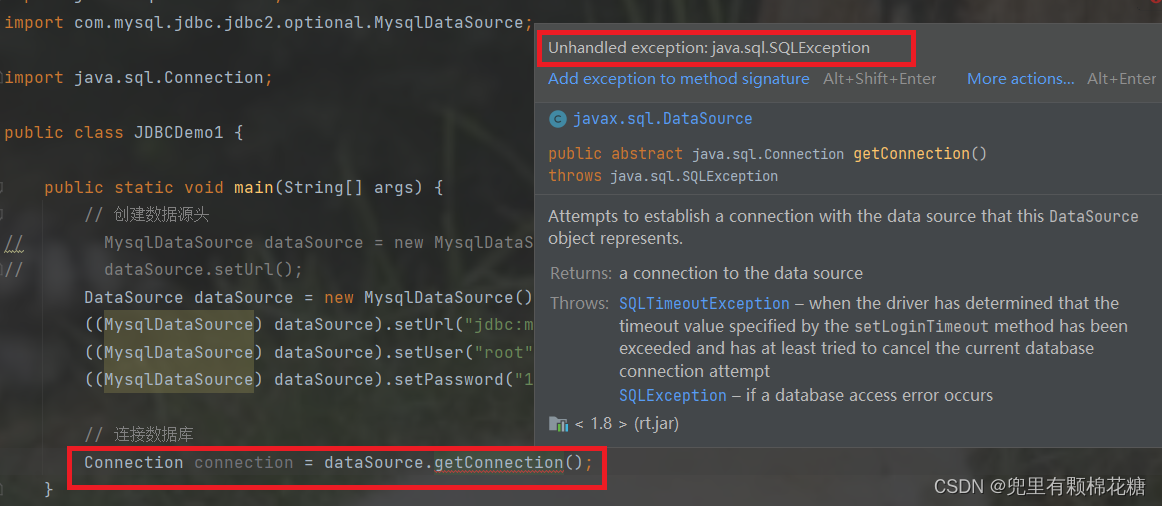
输入代码1: Connection connection = dataSource.getConnection();
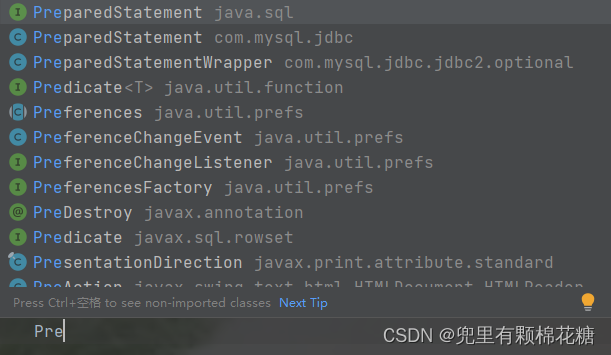
注意:我们输入
Connection的时候必须选择第二个,即java.sql。
同时,我们可以注意到,上面代码抛出了异常(分为受查异常和非受查异常。其中受查异常必须经过我们的手动处理,即要么try catch,要么throws)
我们再来看上述代码抛出的异常(java.sql.SQLException是jdbc中提供的受查异常),按住alt+enter可以抛出异常。
一个java程序,可以连接多个数据库服务器。和每个数据库服务器进行通信都要有独立的连接、通讯。
构造SQL语句
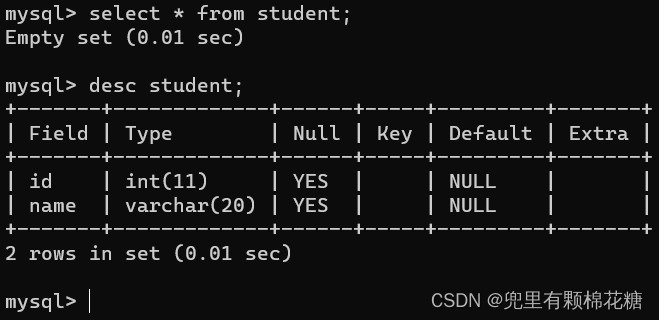
假设我们现在有一张
student(id,name)的学生表,现在向表中进行插入数据。
关键代码:String sql = "insert into student values(1,'张三')";PreparedStatement statement = connection.prepareStatement(sql);
上图中我们选择java.sql库中的PreparedStatement。
解释:
PreparedStatement statement = connection.prepareStatement(sql);
首先我们知道SQL语句是string类型,JDBC提供了Statement(中文是语句的意思)对象让我们把string类型转换为Statement然后再发送给服务器。
但是我们一般会使用PreparedStatement(预处理的语句)对象来替代Statement。
之所以会使用PreparedStatement来代替Statement是因为Statement对象会把SQL语句原封不动的直接发给数据库服务器,此时数据库服务器只能自己来解析SQL语句。
而PreparedStatement对象回先在客户端这边初步解析一下SQL语句(验证语法格式是否符合要求啥的),此时数据库服务器就不需要再做这些检查了,从而降低了数据库服务器的负担。
执行SQL语句
输入代码:int n = statement.executeUpdate();
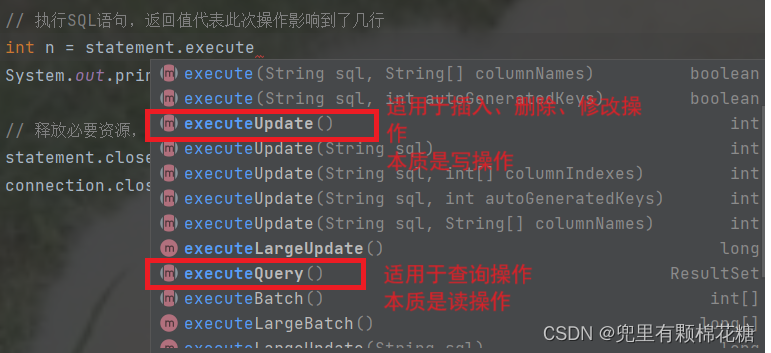
释放必要资源,关闭连接
输入代码:statement.close(); connection.close();
解释:
我们创建的语句对象和连接对象中一般都会持有计算机硬件或者软件上的资源,这些资源我们如果不使用的话就需要及时进行释放。
在Java中虽然有垃圾回收机制来自动释放内存,但是计算机资源中不仅仅包含了内存资源,还包含了一些其它的资源。这些其它的资源(如连接对象中会包含出来内存资源以外的其它计算机资源)就需要我们进行手动释放。
所以我们一般使用close()方法,即一个专门释放资源的方法。
还有一点我们需要注意:先创建的对象后关闭,即后创建的对象先关闭。
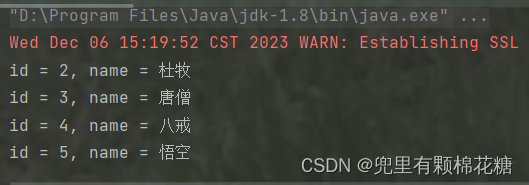
最终运行结果如下:
向数据库中插入数据完整代码
import javax.sql.DataSource;
import com.mysql.jdbc.jdbc2.optional.MysqlDataSource;import java.sql.Connection;
import java.sql.PreparedStatement;
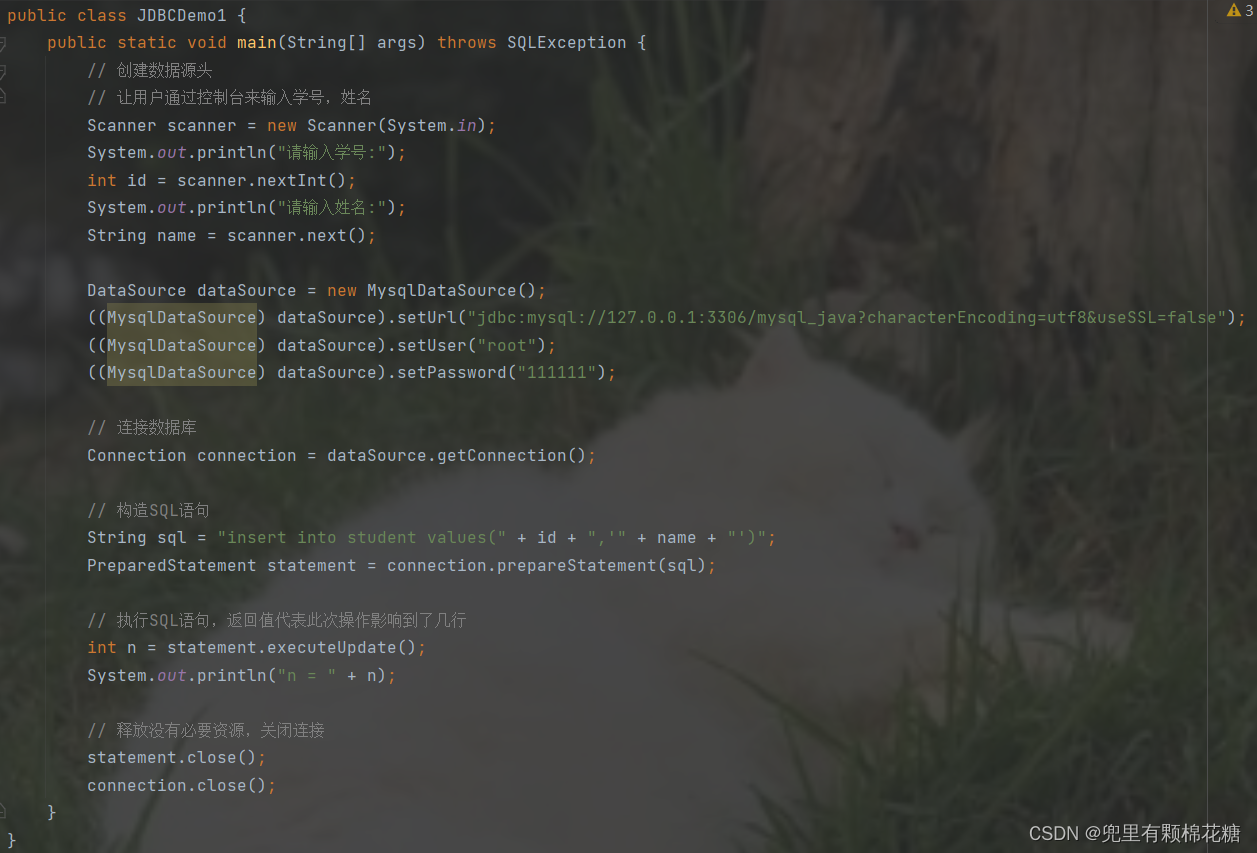
import java.sql.SQLException;public class JDBCDemo1 {public static void main(String[] args) throws SQLException {// 创建数据源头DataSource dataSource = new MysqlDataSource();((MysqlDataSource) dataSource).setUrl("jdbc:mysql://127.0.0.1:3306/mysql_java?characterEncoding=utf8&useSSL=false");((MysqlDataSource) dataSource).setUser("root");((MysqlDataSource) dataSource).setPassword("111111");// 连接数据库Connection connection = dataSource.getConnection();// 构造SQL语句String sql = "insert into student values(1,'张三')";PreparedStatement statement = connection.prepareStatement(sql);// 执行SQL语句,返回值代表此次操作影响到了几行int n = statement.executeUpdate();System.out.println("n = " + n);// 释放没有必要资源,关闭连接statement.close();connection.close();}
}如果我们希望插入的数据能够在运行是发生动态的变化,这种方式当然是可以的;但是我们不希望你这样做,因为那样会使你的代码显得并没有那么整洁。另外拼接字符串的方式也并不是那么的安全。
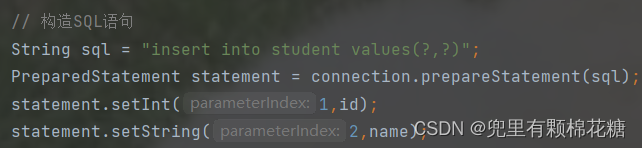
如果我们想要让插入的数据通过控制台发生动态的变化的话,PreparedStatement给我们提供了更为方便的方式(基于占位符的一种方式)比如String sql = "insert into student values(?,?)";。
其中,?是一个占位符,即会占据一个位置,后续PreparedStatement会把变量值带入到?中。
替换方式如下:
上图中代码的写法就会显得代码肥肠粉简单明了。同时在执行过程中,setXXX()方法内部也会进行更为严格的校验(避免出现SQL注入攻击的情况)。
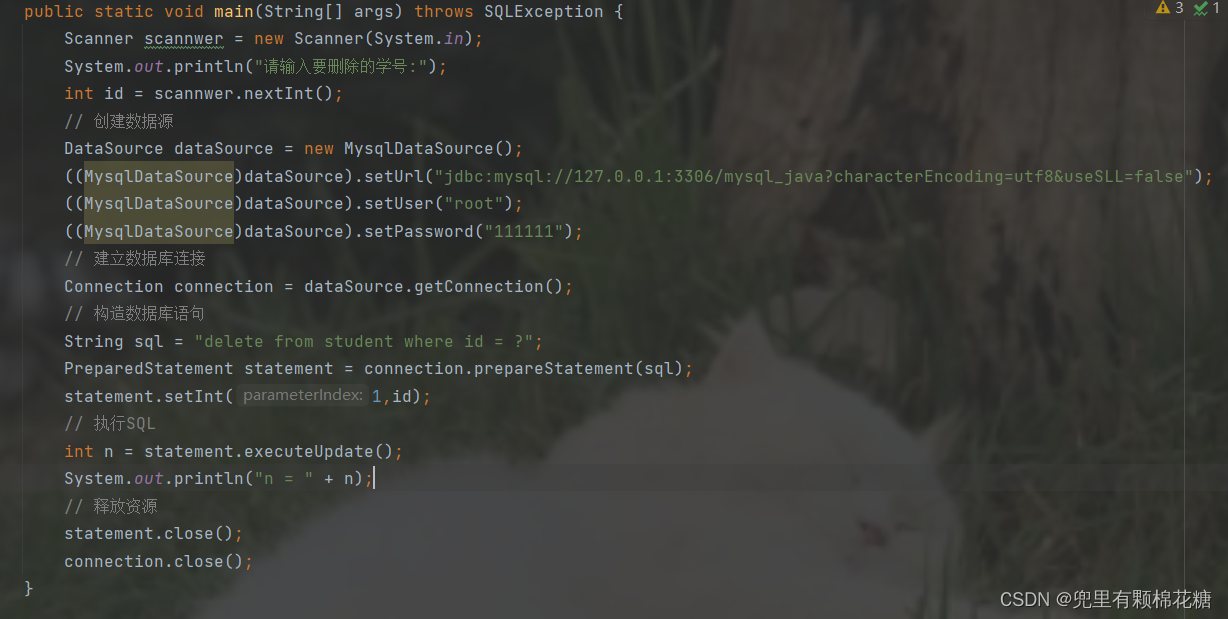
对数据库进行删除操作:
查询数据库中的数据完整代码
对数据库进行查询操作:
关键代码1:ResultSet resultSet = statement.executeQuery();
关键代码2(遍历查询结果集合):
while(resultSet.next())
{int id = resultSet.getInt("id");String name = resultSet.getString("name");System.out.println("id = " + id + ", name = " + name);
}
完整代码如下:
// 查询操作
import com.mysql.jdbc.jdbc2.optional.MysqlDataSource;
import javax.sql.DataSource;
import java.sql.Connection;
import java.sql.PreparedStatement;
import java.sql.ResultSet;
import java.sql.SQLException;public class JDBCDemo3 {public static void main(String[] args) throws SQLException {// 创建数据源DataSource dataSource = new MysqlDataSource();((MysqlDataSource)dataSource).setUrl("jdbc:mysql://127.0.0.1:3306/mysql_java?characterEncoding=utf8&uesSSL=false");((MysqlDataSource)dataSource).setUser("root");((MysqlDataSource)dataSource).setPassword("111111");// 与数据库建立连接Connection connection = dataSource.getConnection();// 构造数据库语句String sql = "select * from student";PreparedStatement statement = connection.prepareStatement(sql);// 执行SQL语句ResultSet resultSet = statement.executeQuery();// 遍历查询结果集合while(resultSet.next()){int id = resultSet.getInt("id");String name = resultSet.getString("name");System.out.println("id = " + id + ", name = " + name);}// 释放资源resultSet.close();statement.close();connection.close();}
}
查询结果如下:
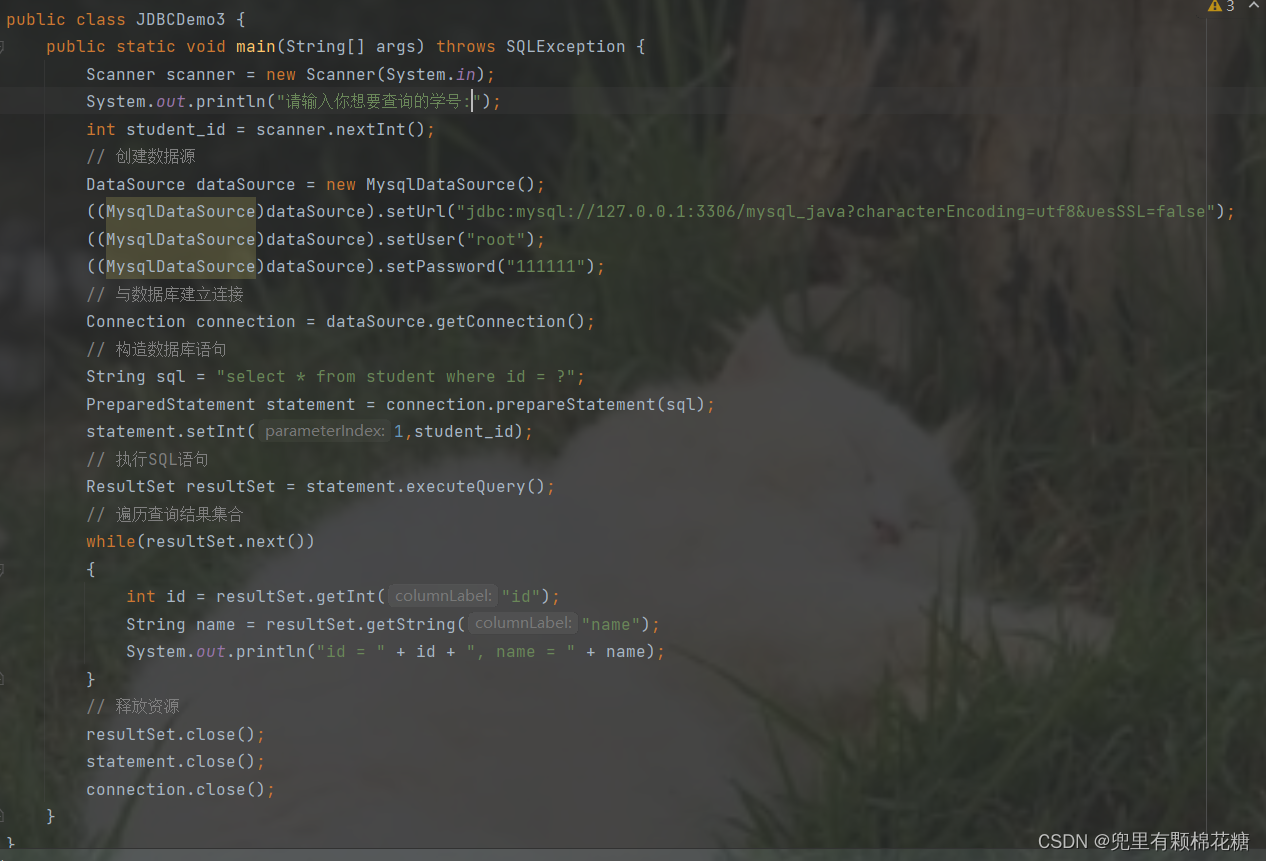
如果我们要查询某一个学号的学生,请看:
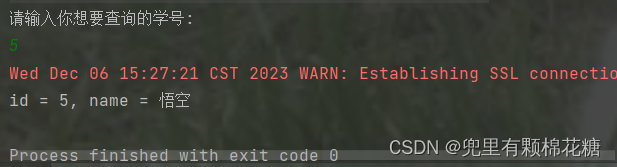
查询结果如下:
另外要注意执行查询操作时要使用
executeQuery()方法。查询操作返回值是一个ResultSet类型的对象来表示是一个表格。(需要我们遍历查询的结果)。
四、JDBC编程注意事项
- 创建数据库连接时,
Connection选择java.sql库中的Connection。 - 创建数据库时不要忘记抛出异常
- 与数据库建立连接时(
Connection connection = dataSource.getConnection();)不要忘记抛出异常(alt+回车) - 准备执行SQL语句的
PreparedStatement对象使用的是java.sql包中的PreparedStatement。
JDBC编程最主要的四个API:
DataSourceConnectionPreparedStatementResultSet(遍历查询结果)
通过上面最主要的4个API,就可以完成JDBC编程。这里并不是太难,但是需要我们经常的去进行练习。
好了,以上就是本文的全部内容了,希望大家多多练习,加强自己的理解。就到这里吧,再见啦友友们!!!