忻州市网站建设_网站建设公司_Java_seo优化
一、问题描述
服务器上运行了几个docker容器,运行个一周就会出现overlay 100%的情况,经查找,是容器里生成了很多core.xxx的文件导致的。
二、解决方法
首先通过以下命令查看:
df -h 可以看的overlay已经100%了,进入到/var/lib/docker目录下
可以看的overlay已经100%了,进入到/var/lib/docker目录下
cd /var/lib/docker/
查看内存使用情况
du -lh --max-depth=1
可以看的主要是/overlay2目录占用的比较大,进入到该目录,继续查看内存使用情况
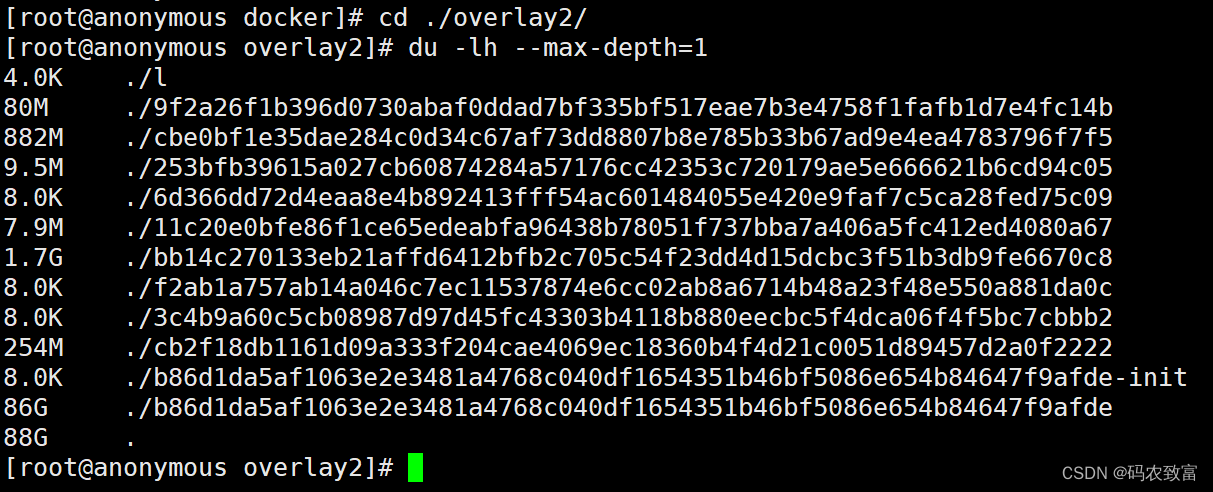
重复使用上面的方式,进行查找

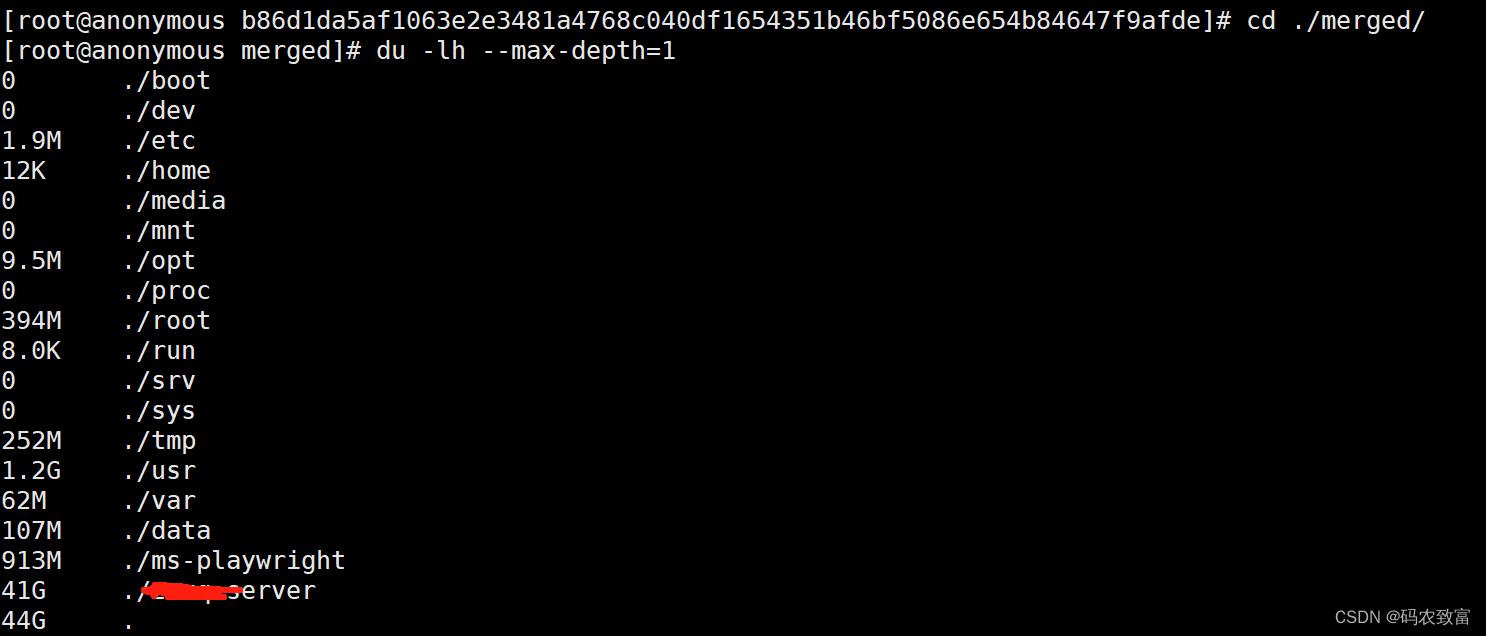
最终查找到如下,生成了一堆的core.xxx文件
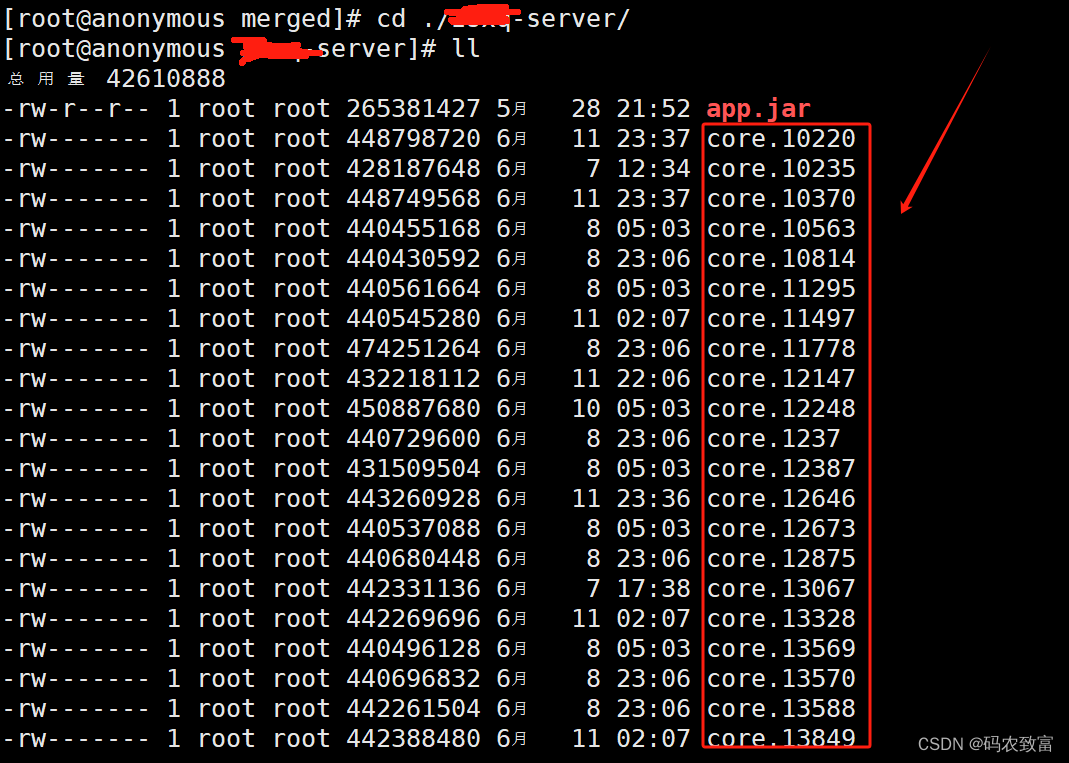 core.xxx文件可能是由于应用程序崩溃或遇到了严重错误导致的,core文件是操作系统保存应用程序崩溃时的内存转储文件,用于调试和分析问题,可以直接执行如下命令,进行删除:
core.xxx文件可能是由于应用程序崩溃或遇到了严重错误导致的,core文件是操作系统保存应用程序崩溃时的内存转储文件,用于调试和分析问题,可以直接执行如下命令,进行删除:
rm -if core.*删除之后,占用就立马降下来了
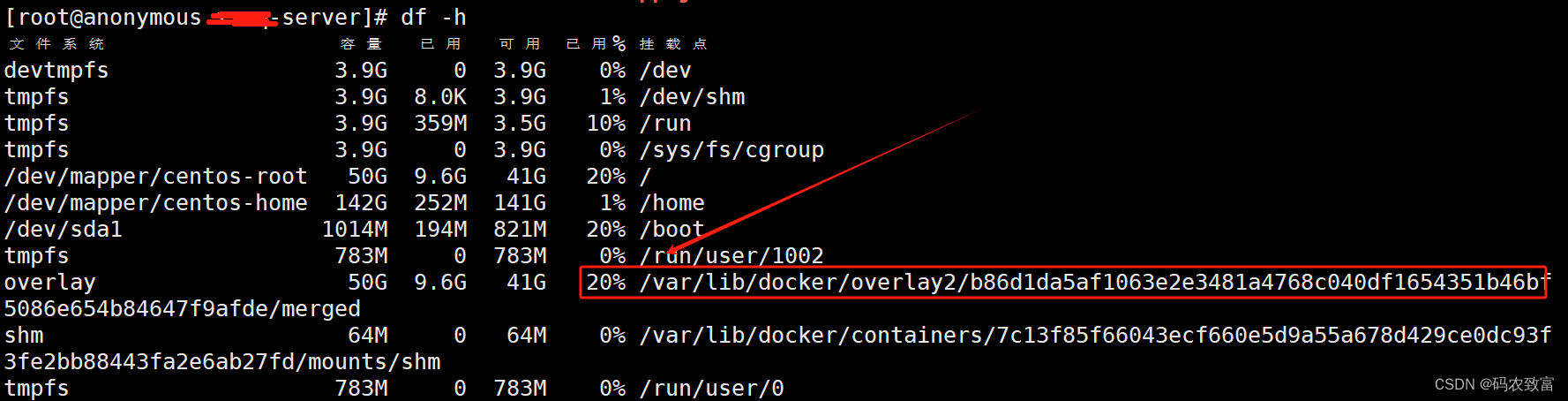
除了core还有日志可能有大文件,删除大的 log 文件
find /var/lib/docker/containers -name *.logcat /dev/null > /var/lib/docker/containers/7c13f85f66043ecf660e5d9a55a678d429ce0dc93f3fe2bb88443fa2e6ab27fd/7c13f85f66043ecf660e5d9a55a678d429ce0dc93f3fe2bb88443fa2e6ab27fd-json.log
