天水市网站建设_网站建设公司_MySQL_seo优化
表单事件
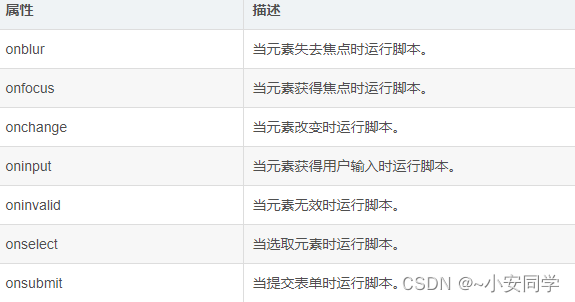
表单事件在HTML表单中触发 (适用于所有 HTML 元素,但该HTML元素需在form表单内):
案例演示1:当文本框获取焦点,文本框背景为红色,当文本框失去焦点,文本框背景为黄色
<!DOCTYPE html>
<html>
<head><meta charset="UTF-8"><title></title>
</head>
<body>
<form><input type="text" id="text">
</form><!-- 在这里写JavaScript代码,因为JavaScript是由上到下执行的 -->
<script>var textInput = document.getElementById("text");/* 当文本框获取焦点,文本框背景为红色 */textInput.onfocus = function () {this.style.background = "red";};/* 当文本框失去焦点,文本框背景为绿色 */textInput.onblur = function () {this.style.background = "green";};
</script>
</body>
</html>
注意:这里为什么要用this,你不用this也可以,就直接
textInput.style.background = "red";也不是不可以的,但是方法的调用规则就是谁调用this,this就指向谁,这样我们就可以简化代码了
案例演示2:当文本框内容改变时,鼠标离开文本框,自动将文本框的内容输出到控制台
<!DOCTYPE html>
<html>
<head><meta charset="UTF-8"><title></title>
</head>
<body>
<form><input type="text" id="text">
</form><!-- 在这里写JavaScript代码,因为JavaScript是由上到下执行的 -->
<script>var textInput = document.getElementById("text");/* 当文本框内容改变时,鼠标离开文本框,自动将文本框的内容输出到控制台 */textInput.onchange = function () {console.log(this.value);};
</script>
</body>
</html>
案例演示3:当文本框内容改变时,立即将改变的内容输出到控制台
<!DOCTYPE html>
<html>
<head><meta charset="UTF-8"><title></title>
</head>
<body>
<form><input type="text" id="text">
</form><!-- 在这里写JavaScript代码,因为JavaScript是由上到下执行的 -->
<script>var textInput = document.getElementById("text");/* 当文本框内容改变时,立即将改变的内容输出到控制台 */textInput.oninput = function () {console.log(this.value);};
</script>
</body>
</html>
案例演示4:如果单击“submit”,则不填写文本字段,将发生警报消息
<!DOCTYPE html>
<html>
<head><meta charset="UTF-8"><title></title>
</head>
<body>
<form><input type="text" id="text" required><input type="submit" value="submit">
</form><!-- 在这里写JavaScript代码,因为JavaScript是由上到下执行的 -->
<script>var textInput = document.getElementById("text");/* 如果单击“submit”,则不填写文本字段,将发生警报消息 */textInput.oninvalid = function () {console.log("请您完善表单内容!");};
</script>
</body>
</html>
案例演示6:当提交表单的时候,在控制台输出“表单提交”
<!DOCTYPE html>
<html>
<head><meta charset="UTF-8"><title></title>
</head>
<body>
<form id="myform"><input type="submit" id="submit">
</form><!-- 在这里写JavaScript代码,因为JavaScript是由上到下执行的 -->
<script>var myform = document.getElementById("myform");/* 当提交表单的时候,在控制台输出“表单提交” */myform.onsubmit = function () {console.log("表单提交");return false;/* 用来阻止表单提交的,你不写它会跳转请求 */};
</script>
</body>
</html>
setTimeout() 方法:延时器
- 第一个参数是要执行的函数。
- 第二个参数指示执行之前的毫秒数。
- 案例演示:单击按钮,等待 3 秒,然后控制台会输出 "Hello"
<!DOCTYPE html> <html> <head><meta charset="UTF-8"><title></title> </head> <body> <button id="btn">按钮</button><!-- 在这里写JavaScript代码,因为JavaScript是由上到下执行的 --> <script>var btn = document.getElementById("btn");btn.onclick = function () {// 创建延时器var timer = setTimeout(function () {console.log("Hello");}, 3000);// 清除延时器// clearTimeout(timer); }; </script> </body> </html>String对象
- length属性演示:可以用来获取字符串的长度
-
var str = "Hello,World!"; console.log(str.length);indexof()方法演示:该方法可以检索一个字符串中是否含有指定内容,如果字符串中含有该内容,则会返回其第一次出现的索引,如果没有找到指定的内容,则返回-1,可以指定一个第二个参数,指定开始查找的位置
-
var str = "Hello,World!"; console.log(str.indexOf("o")); console.log(str.indexOf("o", 5));lastIndexOf()方法演示:该方法的用法和indexOf()一样,不同的是indexOf是从前往后找,而lastIndexOf是从后往前找,也可以指定开始查找的位置
-
var str = "Hello,World!"; console.log(str.lastIndexOf("o")); console.log(str.lastIndexOf("o", 5)); -
substr()方法演示:该方法用来截取字符串
参数:
- 第一个参数:截取开始位置的索引
- 第二个参数:截取的长度
var str = "Hello,World!"; var result = str.substr(6, 6); console.log(result); -
substring()方法演示:可以用来截取一个字符串
-
第一个参数:开始截取位置的索引(包括开始位置)
- 第二个参数:结束位置的索引(不包括结束位置),如果省略第二个参数,则会截取到后边所有的
-
var str = "Hello,World!"; var result = str.substring(1, 4); console.log(result); result = str.substring(1); console.log(result); result = str.substring(1, -1); console.log(result);
split()方法演示:该方法可以将一个字符串拆分为一个数组,需要一个字符串作为参数,将会根据该字符串去拆分数组
var str = "Hello,World!";
var result = str.split(",");
console.log(result);
