长春市网站建设_网站建设公司_服务器维护_seo优化
最近很多用户反馈,升级最新iOS 17系统后打开App Store提示"无法连接",无法正常打开下载APP。

为什么升级后无法连接到App Store?可能是以下问题导致:
1.网络问题导致App Store无法正常打开
2.网络设置问题
3.App Store服务器问题导致无法正常使用
4.系统问题也有可能导致App Store无法正常使用
如果iPhone升级iOS17后App Store无法正常访问,可试试以下这几种办法:
一、网络设置
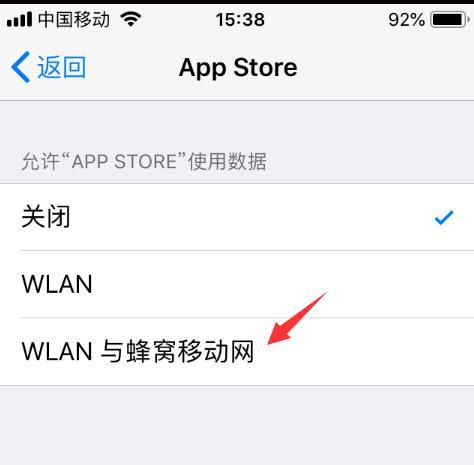
目前苹果默认是自带APP不链接蜂窝网络,可在设置里查看是否设置了不蜂窝网络。设置-蜂窝网络-下划找到App Store-更改为无线局域网与蜂窝数据,即可在移动网络打开App Store,或更换其他wif尝试。
二、还原网络设置
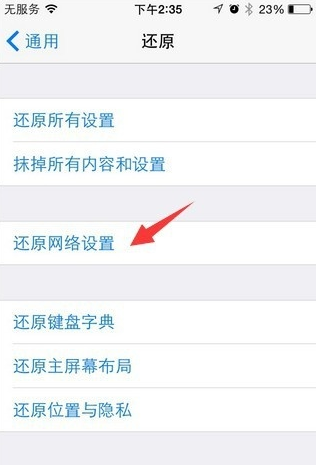
无论是移动网络还是wifi都无法链接App Store的话,可以尝试还原网络设备。
还原网络设置:在手机界面上打开设置,点击通用进入,然后按还原,还原网络设置。重置网络的位置在,“设置”-“通用”-“还原”-“还原网络设置”。
三、查看AppStore服务器状态
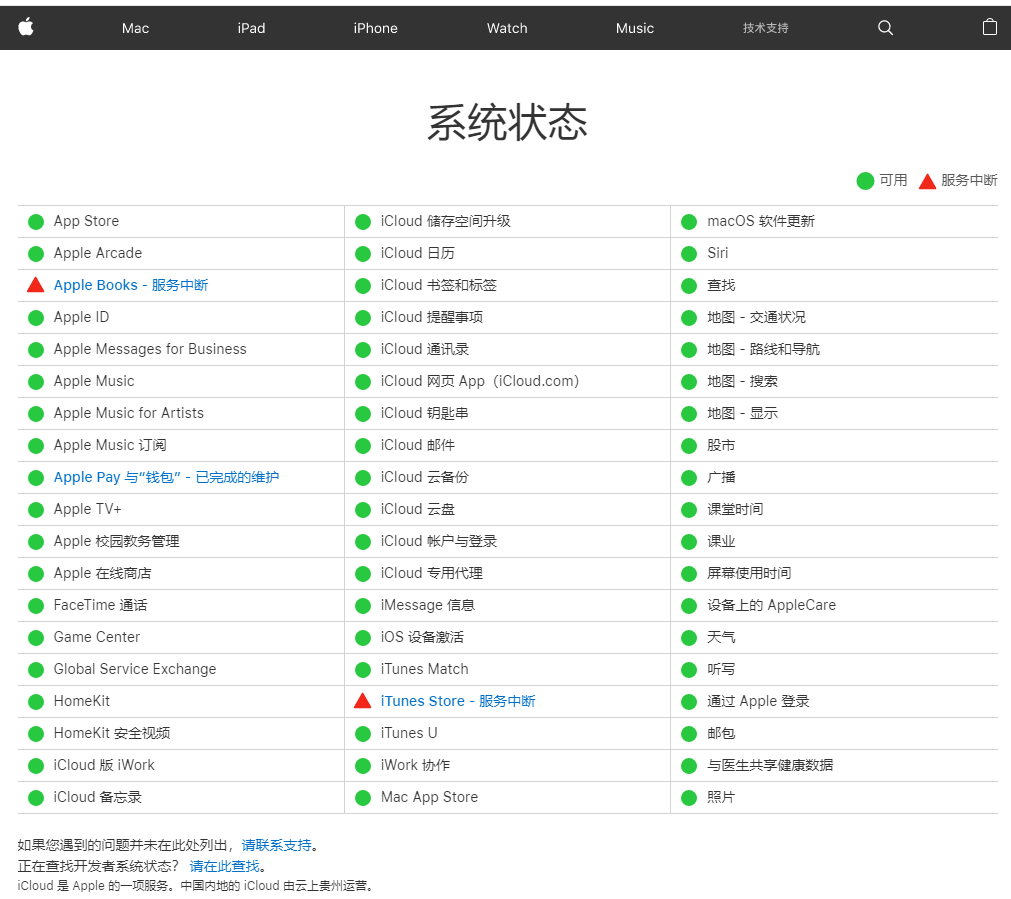
有时候可能AppStore服务器出现问题导致的,我们可以到苹果官网的系统状态页面www.apple.com.cn/cn/support/systemstatus/,进行查看App Store服务器是否正常,如果显示服务中断等异常状态,那就只能等苹果官方修复服务器完成后才可使用App Store了。
四、强制重启
当iPhone升级iOS17后突然打不开App Store,我们还可以尝试强制重启修复。
强制重启操作:快速按下音量加、减键,再长按电源键,直到设备退出白苹果界面,黑屏后再次出现Apple 标志,然后松开按键,直到iPhone正常开机启动。

五、ios系统修复
如果以上办法试了,还是无法正常使用App Store,那就是ios系统有问题,可用牛学长苹果手机修复工具进行系统修复,一键解决App Store无法进入、白苹果、黑屏等150+iOS设备系统问题
第1步:下载安装好牛学长苹果手机修复工具。通过数据线连接设备与电脑,点击“修复iOS系统问题”,选择使用“标准修复”模式。
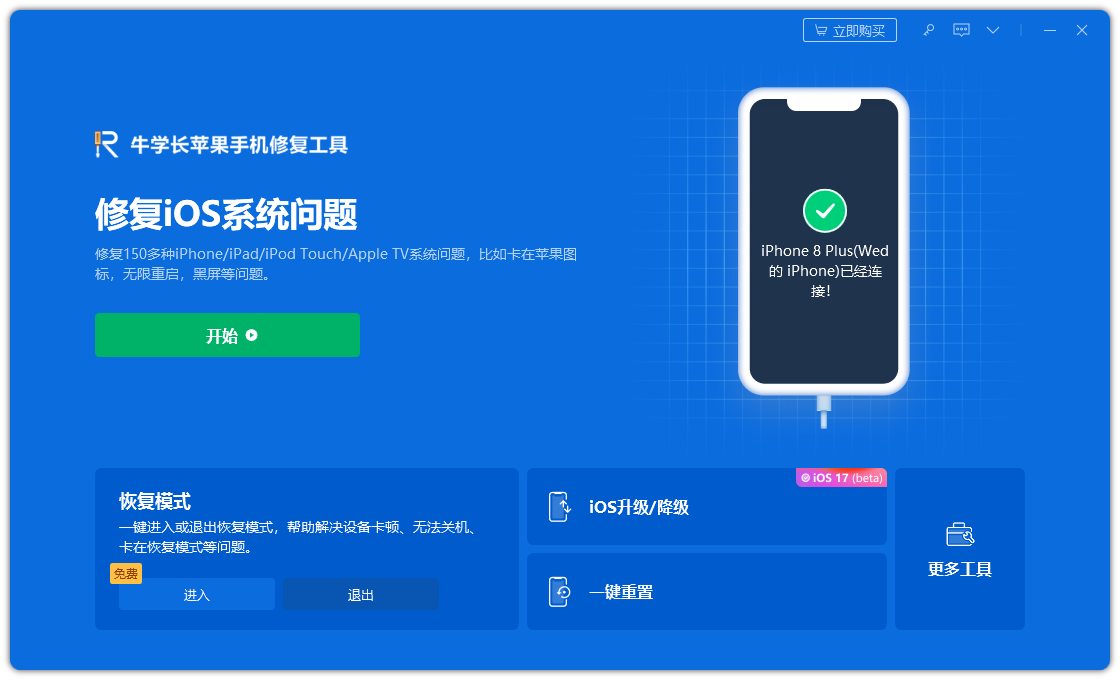
第2步:点击“下载固件”, 默认下载固件为系统提供的最新正式版iOS固件,下载成功后开始更新。
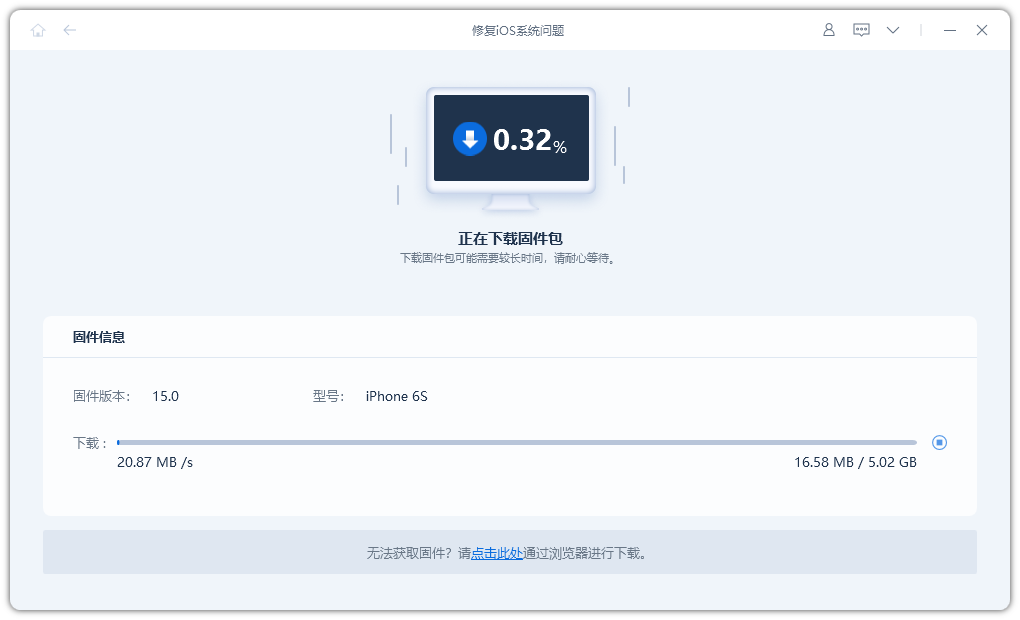
第3步:修复成功。修复过程中注意不要断开数据线,整个过程大概需要10分钟,等待显示“修复完成”即可进入App Store。
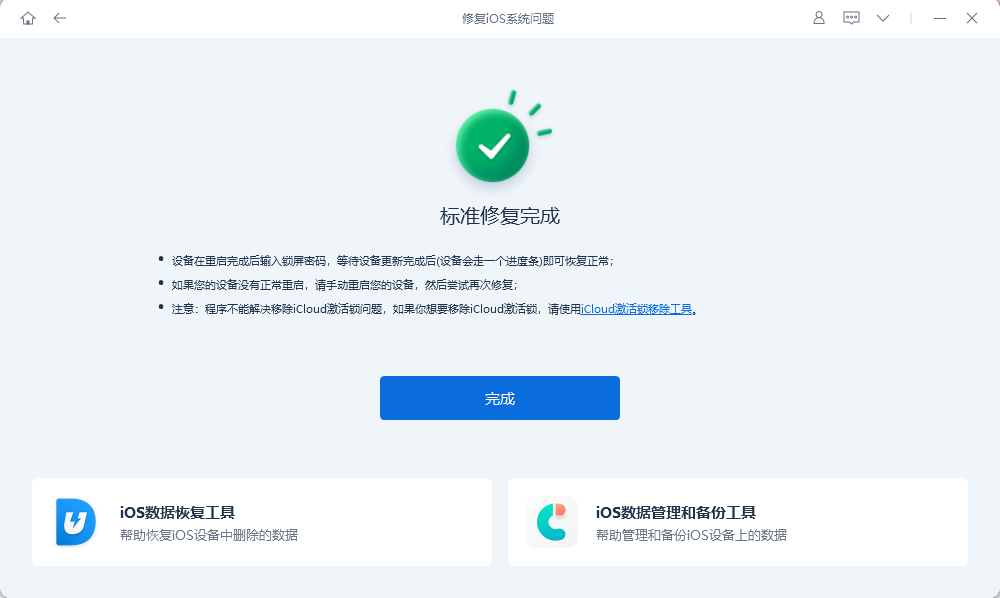
无论是iOS17或iOS16/15出现App Store无法连接的情况,都可以以上办法来解决。
