松原市网站建设_网站建设公司_Logo设计_seo优化
在Entity Framework Core (EF Core)有许多新的功能,最令人期待的功能之一就是批处理语句。那么批处理语句是什么呢?批处理语句意味着它不会为每个插入/更新/删除语句发送单独的请求,它将在数据库的单次请求中批量执行多个语句。在这篇文章中,让我们看看它是如何工作的,并将结果与EF6进行比较。
EF Core将一次准备多个语句,然后在单次请求中执行它们,所以能提供了更好的性能和速度。让我们看看它是如何工作的。我们将借助SQL Server Profiler来捕获实际生成和执行的查询。
插入操作
首先,我们来看看插入语句的行为,以下代码在category表中添加3个记录:
using (var dataContext = new SampleDBContext()) {dataContext.Categories.Add(new Category() {CategoryID = 1,CategoryName = "Clothing"});dataContext.Categories.Add(new Category() {CategoryID = 2,CategoryName = "Footwear"});dataContext.Categories.Add(new Category() {CategoryID = 3,CategoryName = "Accessories"});dataContext.SaveChanges();
}当执行SaveChanges()时,以下是生成语句(通过 SQL Server Profiler 捕获):
exec sp_executesql N'SET NOCOUNT ON;INSERT INTO [Categories] ([CategoryID], [CategoryName])VALUES (@p0, @p1),(@p2, @p3),(@p4, @p5);',N'@p0 int,@p1 nvarchar(4000),@p2 int,@p3 nvarchar(4000),@p4 int,@p5 nvarchar(4000)',@p0=1,@p1=N'Clothing',@p2=2,@p3=N'Footwear',@p4=3,@p5=N'Accessories'您可以看到,没有3条单独的插入语句,它们被组合成一个语句,并且使用表值参数作为值。这里是SQL Server Profiler的屏幕截图:
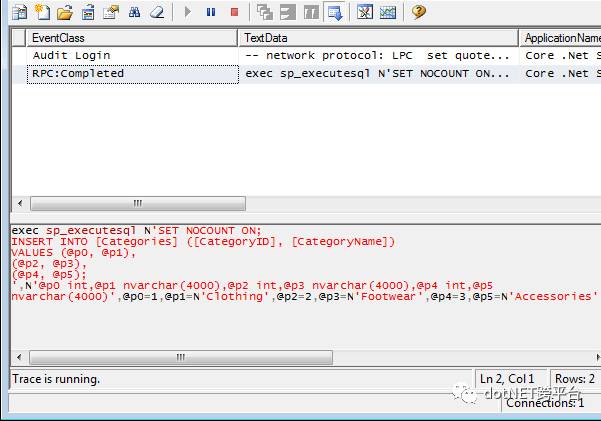
如果我们在EF 6执行相同的代码,那么在SQL Server Profiler中会看到3个单独的插入语句:
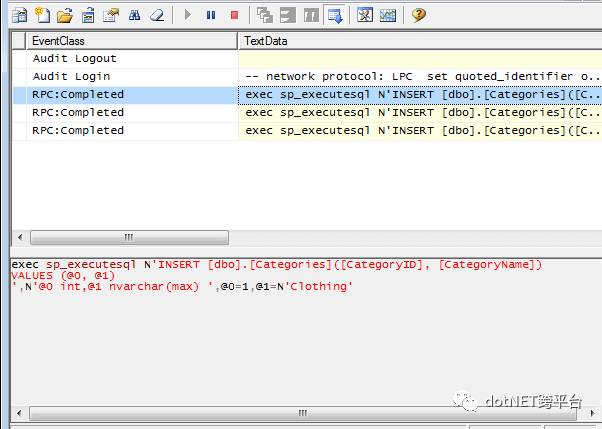
这在性能和速度方面有很大的不同。如果这些查询针对的是云部署的数据库,那么它也将具有更高成本效益。现在,我们看看如果是更新语句会发生什么。
更新操作
以下代码将获得所有category记录列表,然后遍历它们,并为每个类别名称追加“-Test”文本,并保存。在这个时间点上,数据库中只有3条记录。
using (var dataContext = new SampleDBContext()) {List<Category> lst = dataContext.Categories.ToList();
foreach (var item in lst) {item.CategoryName = item.CategoryName + "-Test";}dataContext.SaveChanges();
}并且在EF Core执行时,生成以下查询(通过 SQL Server Profiler 捕获)。
exec sp_executesql N'SET NOCOUNT ON;UPDATE [Categories] SET [CategoryName] = @p0WHERE [CategoryID] = @p1;SELECT @@ROWCOUNT;UPDATE [Categories] SET [CategoryName] = @p2WHERE [CategoryID] = @p3;SELECT @@ROWCOUNT;UPDATE [Categories] SET [CategoryName] = @p4WHERE [CategoryID] = @p5;SELECT @@ROWCOUNT;',N'@p1 int,@p0 nvarchar(4000),@p3 int,@p2 nvarchar(4000),@p5 int,@p4 nvarchar(4000)',@p1=1,@p0=N'Clothing-Test',@p3=2,@p2=N'Footwear-Test',@p5=3,@p4=N'Accessories-Test'您可以看到,有3个更新语句,但都被组合成单条SQL语句。在EF 6执行相同的代码,SQL Server Profiler中将显示3个单独的更新语句:
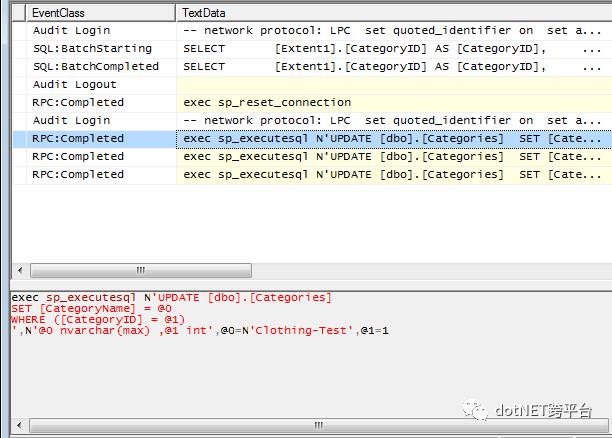
使用EF 6,将有1 + N往返数据库,一次加载数据以及每行数据的修改;但是使用EF Core,保存操作是批量的,所以只有两次往返数据库。
插入、更新、删除混合操作
现在让我们尝试将3个操作混合在一起,看看EF Core和EF 6的行为。以下代码将更新现有记录,并插入2条新记录,最后删除一条记录。
using (var dataContext = new SampleDBContext())
{Category cat = dataContext.Categories.First(c => c.CategoryID == 3);cat.CategoryName = "Accessory";dataContext.Categories.Add(new Category() { CategoryID = 4, CategoryName = "Fragnance" });dataContext.Categories.Add(new Category() { CategoryID = 5, CategoryName = "Sports" });Category catToDelete = dataContext.Categories.First(c => c.CategoryID == 2);dataContext.Entry(catToDelete).State = EntityState.Deleted;dataContext.SaveChanges();
}当执行SaveChanges()时,生成以下查询(通过 SQL Server Profiler 捕获):
exec sp_executesql N'SET NOCOUNT ON;DELETE FROM [Categories]WHERE [CategoryID] = @p0;SELECT @@ROWCOUNT;UPDATE [Categories] SET [CategoryName] = @p1WHERE [CategoryID] = @p2;SELECT @@ROWCOUNT;INSERT INTO [Categories] ([CategoryID], [CategoryName])VALUES (@p3, @p4),(@p5, @p6);',N'@p0 int,@p2 int,@p1 nvarchar(4000),@p3 int,@p4 nvarchar(4000),@p5 int,@p6 nvarchar(4000)',@p0=2,@p2=3,@p1=N'Accessory',@p3=4,@p4=N'Fragnance',@p5=5,@p6=N'Sports'正如您所看到的,有单个DELETE,UPDATE和INSERT语句,但被组合成一个单独的SQL语句。这里是SQL Server Profiler的屏幕截图:

在EF 6的中会发生什么?嗯,您猜对了。您可以通过 SQL Profiler 看到在数据库上执行的单个语句:
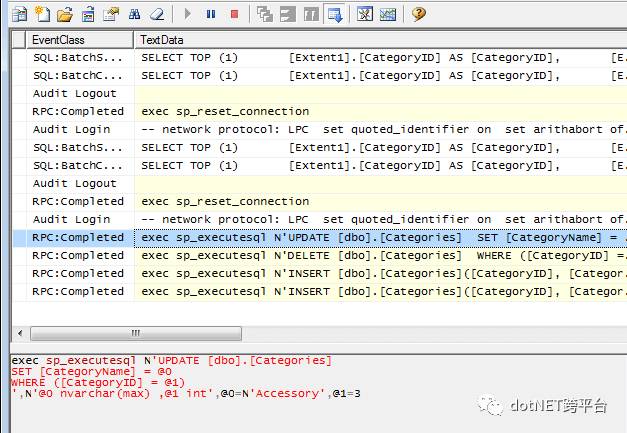
因此,使用EF Core进行批处理可以很大程度提高应用程序的速度和性能。等等,如果大型查询(如要插入500列和100行的表)会发生什么?它会失败吗?
批处理限制取决于您的数据库提供者。例如,SQL Server查询支持的参数最大数量为2100,因此,EF Core在此范围内可以漂亮地工作,并且当批处理限制超出数据库提供程序范围时,将分批查询。但是,在一个查询中批处理所有内容有时不一定是个好方式。有没有办法禁用批处理?
如何禁用批处理
是的,您可以禁用批处理。要禁用批处理,需要修改MaxBatchSize选项,您可以在OnConfiguring方法中进行配置。
protected override void OnConfiguring(DbContextOptionsBuilder optionbuilder){
string sConnString = @"Server=localhost;Database=EFSampleDB;Trusted_Connection=true;";optionbuilder.UseSqlServer(sConnString , b => b.MaxBatchSize(1));
}这里,将最大批量大小设置为1,这意味着批处理现在只能是单条查询。换句话说,它的行为类似于EF 6,要插入3个记录,将有3个单独的插入语句。使用此选项可以定义最大批量大小。
总结
批处理是期待已久的功能,并且社区也多次提出,现在EF Core已经支持,确实很棒,它可以提高应用程序的性能和速度。现在,EF Core本身还不像EF 6那么强大,但随着时间的推移,它将会越来越成熟
相关文章:
Entity Framework Core 生成跟踪列
在Apworks数据服务中使用基于Entity Framework Core的仓储(Repository)实现
Entity Framework Core的贴心:优雅处理带默认值的数据库字段
Entity Framework Core 实现MySQL 的TimeStamp/RowVersion 并发控制
Entity Framework Core 软删除与查询过滤器
Entity Framework Core 命名约定
全文索引 - Pomelo.EFCore.MySql
原文地址:http://www.cnblogs.com/tdfblog/p/batching-of-statement-in-entity-framework-core.html
.NET社区新闻,深度好文,微信中搜索dotNET跨平台或扫描二维码关注

