西安市网站建设_网站建设公司_前后端分离_seo优化
1、锁的粒度分类
1、全局锁
一般用于数据库备份,整个库只读
FLUSH TABLES WITH READ LOCK2、表级锁
细分为:
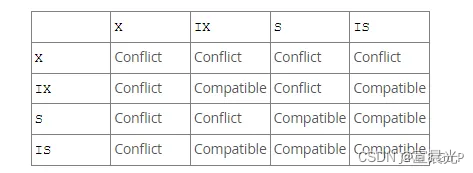
1)意向锁 Intention
事务A对表加行级锁,这行记录就只能读不能写。
事务B申请增加表级锁,如果他申请成功了,那么他就可以修改表中的任意一行记录。这就发生了冲突。
1、意向锁并不是直接锁定资源,而是为通知其他事务,以防止它们在资源上设置不兼容锁。
2、意向锁并不是直接由用户请求的,而是由 MySQL 管理的。
- 意向共享锁 IS:事务打算设置共享锁(读锁),此时不希望其他事务设置排他锁
- 意向排他锁 IX
在触发意向锁的事务提交或者回滚后释放
2)AUTO_INC 锁
在表主键设置ID自增,插入或删除数据时,锁定表。在插入操作完成后立即释放,而不是在事务结束时释放。所以高并发下,不会引起自增异常。
3)字典锁
一般在DDL 处理表字段、索引、事务等数据库定义语句时,添加锁
细分为:
- 1)共享字典锁(SHARED-MDL ):允许其他事务读
- 2)排他字典锁:禁止其他事务读、写
4)表级排他/共享锁
5、行级锁
行级锁都是锁定索引。
针对主键索引,如果表中不存在,则选择唯一非空索引,否则选择隐藏字段 row_id
1)Record Lock:行锁
2)Gap Lock:范围锁 左开右开
3)Next-Key Lock:范围锁 左开右闭
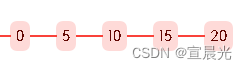
update t where id = 6
由于表 中没有 id=6 的记录,则产生临键锁(5,10】,并且是等值查询,优化为(5,10)
select * from t where id>=10 and id<11 for update
产生间隙锁(10,15)
select * from t where id>10 and id<16 for update
产生临键锁(10,15】
2、锁级别分类
共享锁 S:设置读锁,允许其他事务读取,禁止其他事物申请写锁
SELECT ... LOCK IN SHARE MODE;
排他锁 X:设置写锁,禁止其他事物设置读、写锁
SELECT ... FOR UPDATE;
3、锁的使用方式
1)乐观锁:通过CAS的机制,使用参数status、version等字段比对前后值
2)悲观锁:进行实际的加锁操作
