太原市网站建设_网站建设公司_Windows Server_seo优化
一、引言
在数字化时代,数据是App推广和运营的核心驱动力。然而,如何准确获取、分析并应用这些数据,却成为了许多开发者和营销人员面临的痛点。Xinstall作为一款专业的App全渠道统计服务商,致力于提供精准、高效的数据解决方案,助力广大开发者和营销人员打破数据壁垒,实现业务增长。
二、ASA全链路数据归因:洞察广告效果,优化运营策略
在App推广过程中,广告效果的评估至关重要。Xinstall的ASA归因功能能够监测到从广告曝光、点击、安装到激活后的注册、活跃、留存、付费等全链路数据,帮助广告主直观评估广告效果,分析优化运营策略。这种全方位的数据归因,使得广告主能够更加精准地把握用户需求,提升广告投放效果。
三、全渠道统计:一站式解决数据分散问题
在多渠道投放广告时,数据分散、难以整合是许多广告主面临的难题。Xinstall作为App全渠道统计服务商,能够全面支持ASA归因、H5渠道、广告平台渠道、自然下载等多种渠道的统计。通过整合处理各渠道的归因数据,使得每次App下载与激活都能精准归因到正确的渠道上,所有渠道的转化效果一目了然。这种一站式的数据统计解决方案,大大简化了广告主的数据处理工作,提高了数据分析的效率。
四、支持归因数据导出:加强业务整合与归纳分析
在获得数据之后,如何进行有效的数据分析成为关键。Xinstall支持包含具体渠道、归因结果以及后续行为事件的数据导出功能。广告主可以随时将全渠道任意数据导入自身BI系统中,进一步加强业务整合与归纳分析。这种数据导出功能使得广告主能够更加灵活地运用数据,发现业务机会,制定更加精准的营销策略。
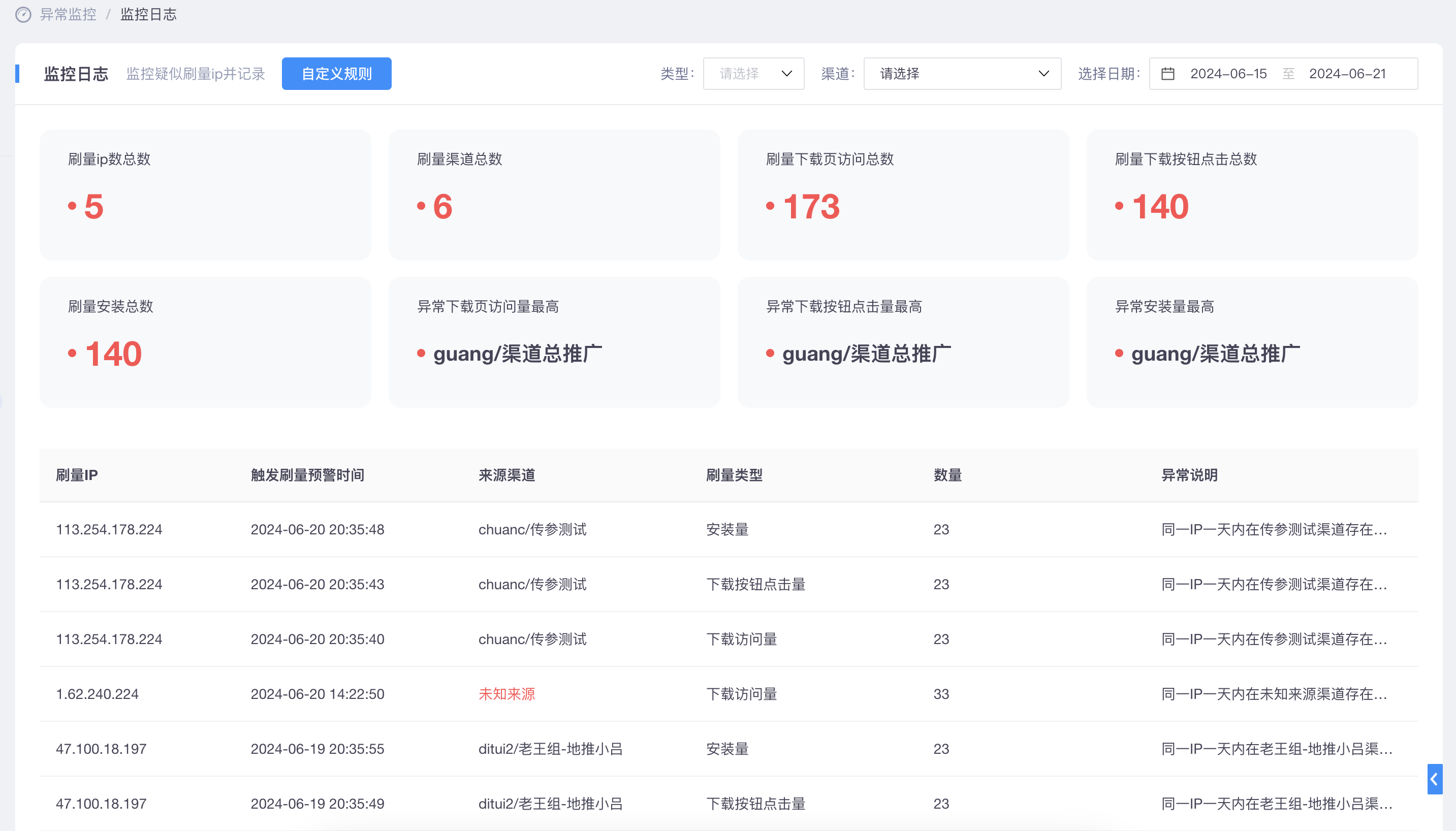
五、全方位渠道作弊监控:保障数据纯净与投放效果
在广告投放过程中,渠道作弊是一个不容忽视的问题。Xinstall提供全方位的渠道作弊监控功能,通过技术手段对广告渠道进行实时监控和数据分析,及时发现并处理作弊行为。这种监控功能保障了数据的纯净性和广告投放的效果,让广告主能够放心投放广告,实现业务增长。
六、激活社交关系链:提升用户活跃与粘性
除了数据统计和监控功能外,Xinstall还提供了关系链归因功能。通过关系链归因,广告主可以筛选用户社交关系、维护社交关系、丰富社交关系以及建立平台信任感和归属感。这种功能不仅提升了用户的活跃度和粘性,还拓宽了盈利模式,丰富了用户画像维度。
七、结语
在数字化时代,数据是App推广和运营的核心驱动力。Xinstall作为一款专业的App全渠道统计服务商,通过提供精准、高效的数据解决方案,助力广大开发者和营销人员打破数据壁垒,实现业务增长。无论是ASA全链路数据归因、全渠道统计、数据导出、渠道作弊监控还是关系链归因功能,Xinstall都能够满足广告主的不同需求,让数据成为推动业务增长的重要力量。
