宜宾市网站建设_网站建设公司_Vue_seo优化
1 连接过程 - 握手
传统的 C/S 架构下,Client 和 Server 通常会建立一条抽象的 Connection,用来进行两端的通信。
UE 的官方文档中提供了 Client 连接到 Server 的示例 ,简单来说分为如下几步:
- 打包构建好 Client 和 Server 进程
- 启动 Server 进程,启动参数为
./Binaries/Win64/<PROJECT_NAME>Server.exe -log - 启动 Client 进程,启动参数为
./Binaries/Win64/<PROJECT_NAME>Client.exe 127.0.0.1:7777 -WINDOWED -ResX=800 -ResY=450
默认情况下,专用服务器在 localhost Ip 地址(
127.0.0.1)的端口7777处监听。可以添加命令行参数-port=<PORT_NUMBER>,更改专用服务器的端口。如果要更改服务器正在使用的端口,则还需要更改将客户端连接到服务器时的端口。
1.1 启动 Server
Client 连接到 Server 的前提是 Server 启动完毕,监听完毕端口,准备好接收连接了。UE 中监听的核心接口如下:
bool UWorld::Listen( FURL& InURL ); |
其接口核心参数为一个 FURL ,UE 中会根据启动参数和配置等构建一个 FURL,其结构如下 (只展示部分变量):
//URL structure. | |
USTRUCT() | |
struct FURL | |
{ | |
// Optional hostname, i.e. "204.157.115.40" or "unreal.epicgames.com", blank if local. | |
UPROPERTY() | |
FString Host; | |
// Optional host port. | |
UPROPERTY() | |
int32 Port; | |
// Map name, i.e. "SkyCity", default is "Entry". | |
UPROPERTY() | |
FString Map; | |
// Options. | |
UPROPERTY() | |
TArray<FString> Op; | |
} |
可以看到里面有关键的 Host 和 Port 等信息。
Listen 接口具体做了什么呢?
- 通过
UEngine:: CreateNamedNetDriver创建 NetDriver,主要驱动网络同步 UNetDriver::InitListen解析 FURL,监听端口
网络相关的流程在这里开始就交付给了UNetDriver,显然它是一个比较重要的网络管理类,这里简单看下其结构
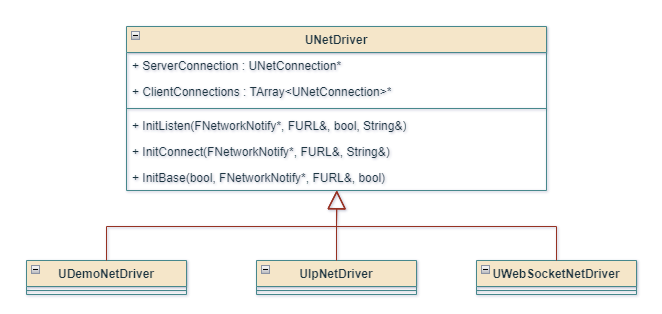
可以看到主要负责:
- Server 端初始化监听端口
- 初始化连接
- 管理 UNetConnection,UNetConnection 显然就是抽象出来的连接
- 这里有 ServerConnection 和 ClientConnections,当拥有 ServerConnection 时表示当前是 Client 端,拥有 ClientConnection 时表示当前时 Server 端
同时其派生了不同的类,如:
- UDemoNetDriver:用来支持游戏录像和回放(类似守望先锋的击杀回放)
- UWebSocketNetDriver:用于实现 WebSocket 协议的网络通信。WebSocket 是一种基于 TCP 的网络协议,允许在客户端和服务器之间进行双向通信,可以实现实时通信和数据传输。通过使用
UWebSocketNetDriver,可以在 UE4中使用 WebSocket 协议进行网络通信 - UIpNetDriver:用于实现基于 IP(Internet Protocol)的网络通信
Server 端完整的绑定端口监听的流程大致如下:
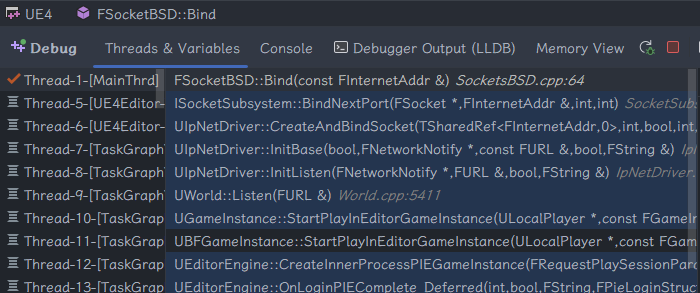
可以看到其实和普通的 C++ 创建 TCP C/S 连接类似,最终都是创建一个 Socket 并且 Bind 到指定端口。
1.2 Client 初始化
客户端启动之后,也是类似的流程,创建 NetDriver 驱动网络相关的流程,对比 Server,其多了一个 UPendingNetGame 的对象。UPendingNetGame 类是一个用于处理网络游戏连接过程的类。它在客户端尝试连接到服务器时创建,并在连接成功或失败后销毁。
关于 UPendingNetGame
用处:
UPendingNetGame 主要负责处理客户端与服务器之间的连接流程。主要功能包括:
a. 处理连接请求:客户端向服务器发起连接请求时,UPendingNetGame 负责处理这个请求,包括创建套接字连接、发送握手请求等。
b. 加载关卡:在连接过程中,若服务器需要客户端加载一个关卡,UPendingNetGame 负责处理这个请求,包括加载关卡资源、同步关卡状态等。
c. 状态同步:在连接过程中,UPendingNetGame 负责与服务器进行状态同步,包括玩家数据、游戏规则等。
d. 错误处理:若连接过程中出现错误,如超时、被拒绝等,UPendingNetGame 负责处理这些错误,通知用户并做出相应处理创建与销毁:
a. 创建:当客户端尝试连接到服务器时,会创建一个 UPendingNetGame 实例。
b. 销毁:当客户端成功连接到服务器并完成状态同步后,UPendingNetGame 完成其任务并被销毁。如果连接过程中出现错误,如超时、被拒绝等, UPendingNetGame 也会在处理完错误后被销毁
Client 的初始化流程大致如下:
- UEngine::Browse 解析 FURL
- UPendingNetGame::InitNetDriver 初始化网络驱动
- UIpNetDriver::InitConnect 初始化连接
- 创建 UIpNetConnection
- UIpNetConnection::InitLocalConnection 初始化连接信息
- 调用 Connection 的 Handler 的 BeginHandshaking 发握手包
其大致执行堆栈如下:
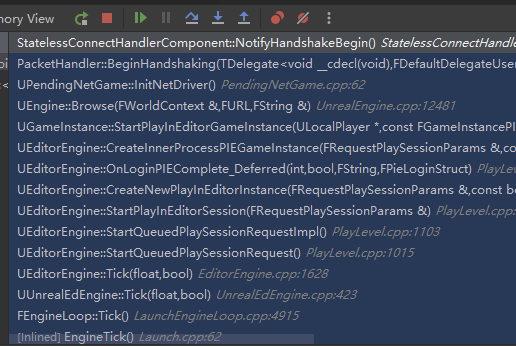
1.3 Server 收包
Server 端上 PacketHandler 处理的数据包的结构如下:
/** | |
* Represents a view of a received packet, which may be modified to update Data it points to and Data size, as a packet is processed. | |
* Should only be stored as a local variable within functions that handle received packets. | |
**/ | |
struct FReceivedPacketView | |
{ | |
/** View of packet data, with Num() representing BytesRead - can reassign to point elsewhere, but don't use to modify packet data */ | |
TArrayView<const uint8> Data; | |
/** Receive address for the packet */ | |
TSharedPtr<FInternetAddr> Address; | |
/** Error if receiving a packet failed */ | |
ESocketErrors Error; | |
}; |
1.3.1 收包流程
Server 监听完端口之后就要处理客户端发过来的连接请求,由于是 UDPSocket,所以只需要简单的 Bind + RecvFrom 就能接收数据了。其主流程主要由 NetDriver 的 TickDispatch 驱动,如下:
UIpNetDriver::TickDispatch- FPacketIterator (UIpNetDriver*) ++,UE 实现了一个 Iterator 遍历消费 Socket 的 Packet
UIpNetDriver::AdvanceCurrentPacketFPacketIterator::ReceiveSinglePacket迭代器收包- UIpNetDriver 中检查 SocketReceiveThreadRunnable 如果存在这个线程(默认情况下应该是没开的,这个时候就相当于这个线程的逻辑在 GameThread 跑了),从 SocketReceiveThreadRunnable->ReceiveQueue 这个 Packet 队列弹出,这里主要是区分用 GameThread 还是用 SocketReceiveThread 来取包。
FReceiveThreadRunnable::Run本身是生产者,可以将 ReceiveQueue 理解为一个数据中间件,IpNetDriver 的 TickDispatch 则是消费者,一直消费 ReceiveQueue 的数据- ReceiveQueue 在
SocketReceiveThreadRunnable线程中一直使用FSocket::RecvFrom(抽象接口,大部分情况下都是为FSocketBSD::RecvFrom)接收数据,其底层实现就是使用recvfrom这个操作系统接口
- UIpNetDriver 中检查 SocketReceiveThreadRunnable 如果存在这个线程(默认情况下应该是没开的,这个时候就相当于这个线程的逻辑在 GameThread 跑了),从 SocketReceiveThreadRunnable->ReceiveQueue 这个 Packet 队列弹出,这里主要是区分用 GameThread 还是用 SocketReceiveThread 来取包。
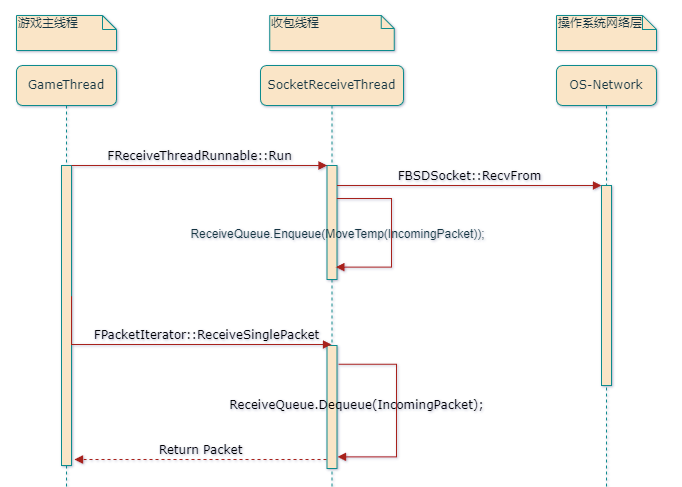
SocketReceiveThreadRunnable 默认是没有打开的,官方说明如下:
// If the cvar is set and the socket subsystem supports it, create the receive thread.CVarNetIpNetDriverUseReceiveThread.GetValueOnAnyThread() != 0 && SocketSubsystem->IsSocketWaitSupported()
1.3.2 处理客户端连接
首先 Server 需要检查这个 Packet 是否已经有连接了,这里引出一个问题,Server 端是如何管理和查询 Connection 的?主要是通过解析 Packet 的 Address,在 UNetDriver 中查询缓存地址映射关系。
// 声明 | |
class UNetDriver { | |
TMap<TSharedRef<const FInternetAddr>, UNetConnection*, FDefaultSetAllocator, FInternetAddrConstKeyMapFuncs<UNetConnection*>> MappedClientConnections; | |
} | |
// 使用 | |
const TSharedRef<const FInternetAddr> FromAddr = ReceivedPacket.Address.ToSharedRef(); | |
UNetConnection** Result = MappedClientConnections.Find(FromAddr); |
接下来是处理 Packet
- TickDispatch 正常消费到 Packet 之后,要确定 Packet 该丢给哪一层
- 由于未建立连接,下一层交由
UIpNetDriver::ProcessConnectionlessPacketPacketHandler::IncomingConnectionless校验 Packet 正确性PacketHandler::Incoming_Internal- 遍历
HandlerComponent对包进行处理 StatelessConnectHandlerComponent::IncomingConnectionless处理无连接的 PacketStatelessConnectHandlerComponent::ParseHandshakePacket检查是否为握手包,根据 Packet 时间戳确定是否是 bInitialConnect- 握手包回一个 Challenge 包
StatelessConnectHandlerComponent::SendConnectChallenge
- 遍历
StatelessConnectHandlerComponent::HasPassedChallenge校验- 检查是否是重连,处理重连逻辑
- 创建
UIpConnection UIpConnection::InitRemoteConnection- UNetConnection 的 ClientLoginState 初始化为
EClientLoginState::Type::LoggingIn
- UNetConnection 的 ClientLoginState 初始化为
FNetworkNotify::NotifyAcceptedConnection通知接收连接UNetDriver::AddClientConnection添加UIpConnection
关于 Challenge
Challenge 消息是 Unreal Engine 4(UE4)中的一种网络消息,用于在客户端和服务器之间进行身份验证。在 UE4 中,客户端和服务器之间的通信是通过一种称为 Unreal Network Protocol(简称 UNet)的协议实现的。UNet 通过在客户端和服务器之间发送各种类型的网络消息来管理通信。在 UE4 中,当客户端第一次连接到服务器时,服务器会向客户端发送一个 Challenge 消息,其中包含一个随机生成的 Challenge 令牌。客户端必须将这个 Challenge 令牌使用预共享密钥(PSK)进行签名,并将签名后的结果发送回服务器。服务器会验证签名是否正确,如果正确,则表示客户端是一个合法的用户,并将向客户端发送一个 ChallengeAck 消息,其中包含服务器的签名和一些其他的验证信息。客户端必须验证 ChallengeAck 消息是否正确,并将消息发送回服务器,以便进行最终的身份验证。
关于 NMT_Hello
可以看到收到客户端连接包之后,除了回复正常的 Ack 包之外,会主动给客户端发送一个 NMT_Hello 包,这里的 NMT_Hello 是一个枚举。UE4 中 NMT 开头的枚举是指 NetworkMessageTypes,是 Unreal Engine 4(UE4)中用于管理网络消息类型的一组枚举。在 UE4 中,网络消息是通过一种称为 Unreal Network Protocol(简称 UNet)的协议进行传输和管理的。UNet 通过在客户端和服务器之间发送各种类型的网络消息来管理通信。通过接收不同的 NMT 消息,从而在客户端服务器连接过程中,不同阶段执行不同的操作,比如当前收到这个消息应该加载地图或者创建 PlayerController。
1.4 握手小结
至此大致梳理完了 Client 和 Server 的握手流程:
- 创建网络驱动 UNetDriver
- Server 端 Listen
- Client 端先创建 UIpConnection 发起连接
- Server 端接收连接,回复 ConnectChallenge 包
- Client 收包,回复 ChallengeResponse 包
- Server 回复 ChallengeAck
- 握手完毕
其中重点内容主要有: - UNetDriver 是网络同步核心,用于驱动网络同步
- Client 会有一个
UPendingNetGame在正式连接前驱动握手过程 - Client 会先创建 Connection,Server 收到后才创建对应的 Connection,Connection 用于收发握手过程中的数据包
- Server 和 Client 收包底层使用 Connection 的 PacketHandler
- 握手过程主要利用
PacketHandler的 HandlerComponent 中的StatelessConnectHandlerComponent,其负责整个握手过程,此外 PacketHandler 的 HandlerComponent 可以挂载各种组件来支持对数据包的处理,比如 RSA,加密解密等
双方完整握手的流程如下:
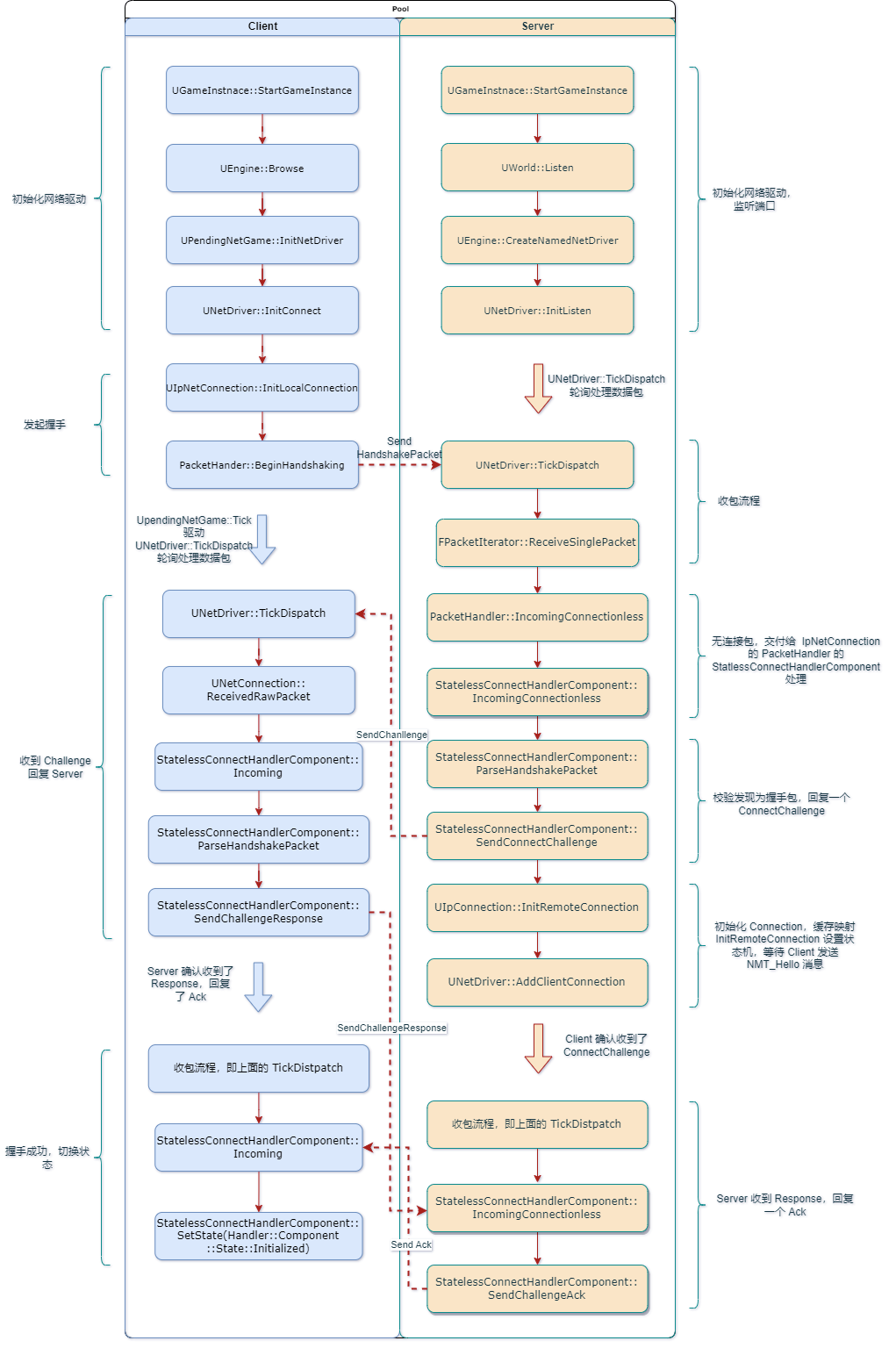
1.5 QA
1.5.1 丢包处理
握手过程中显然有丢包的可能,在 CS 握手过程中,大致发送的 Packet 如下:
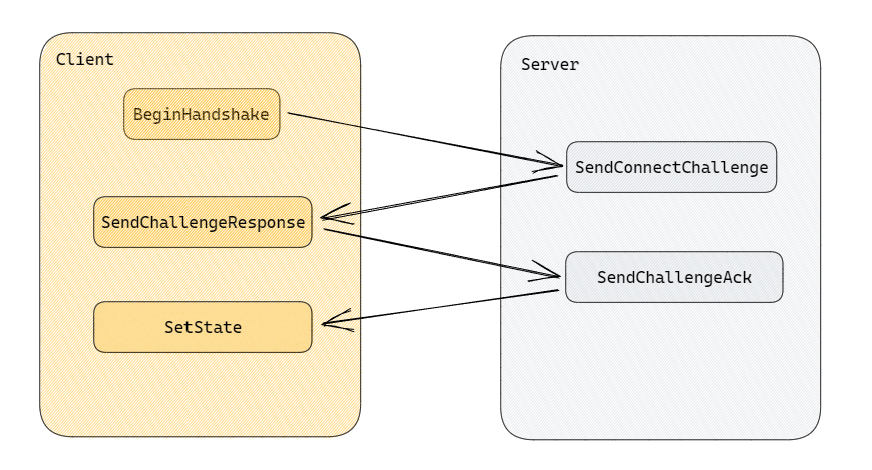
Client 主要发送两个包,Handshake 和 ChallengeResponse,当 Client 没有收到回应时,对应阶段在 StatelessConnectHandlerComponent::Tick 都会有一个重发机制。参考代码如下:
void StatelessConnectHandlerComponent::Tick(float DeltaTime) | |
{ | |
if (Handler->Mode == Handler::Mode::Client) | |
{ | |
// ... 省略一些代码 | |
if (LastSendTimeDiff > 1.0) | |
{ | |
if (State == Handler::Component::State::UnInitialized) | |
{ | |
NotifyHandshakeBegin(); | |
} | |
else if (State == Handler::Component::State::InitializedOnLocal && LastTimestamp != 0.0) | |
{ | |
SendChallengeResponse(LastSecretId, LastTimestamp, LastCookie); | |
} | |
} | |
} |
1.5.2 连接过程用到了哪些关键 Class
大致如下:

2 连接过程 - Enter Game
握手完毕后就要准备一些 Gameplay 层的相关操作,比如加载地图等,Packet 对于应用层还是太底层了,UE 为此引入了 Bunch 和 Channel 的概念
2.1 Bunch
2.1.1 Bunch 和 Packet 的区别
首先 Bunch 和 Packet 的关系如下:
- Bunch:Bunch是UE4中的一个基本网络数据单位。它可以被看作是一组数据的集合,这些数据代表了某个特定时刻的游戏状态变化。Bunch充当了一种中介,将游戏的状态信息打包成可以在网络上发送和接收的格式。它包含了一些关于对象、事件和属性的信息,以及一些控制网络通信的元数据。
- Packet:Packet是一个更大的网络数据单位,用于在网络上实际传输数据。一个Packet通常包含多个Bunch,以及其他一些网络层所需的信息,如包序号、时间戳等。Packet在网络上发送时,会被分割成更小的数据包,以适应各种网络环境和传输协议。
Bunch和Packet之间的关系是层次性的。Bunch负责打包游戏状态的变化,而Packet负责在网络上传输这些Bunch。在数据传输过程中,Bunch被组合成Packet,Packet在发送端被编码为可以在网络上传输的二进制数据,然后在接收端被解码还原为Bunch,以便在游戏中应用状态变化。
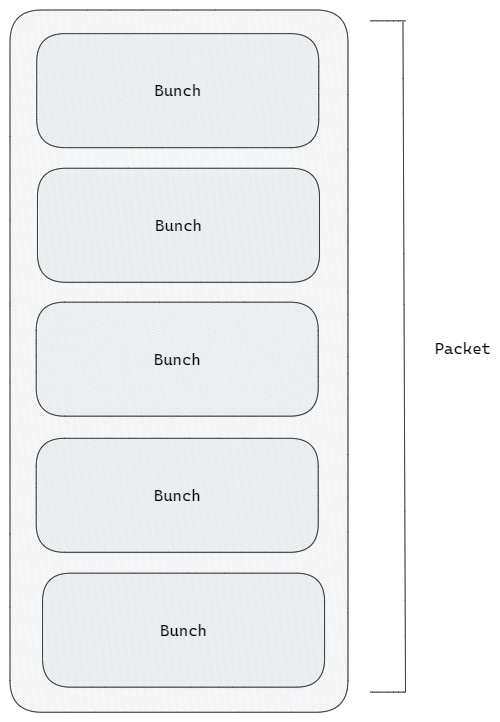
2.1.2 Bunch 的结构
Bunch 分为 FInBunch 和 FOutBunch,根据这个名字可以看出分别对应收到的 Bunch 结构和 发送的 Bunch 结构,其继承链如下:
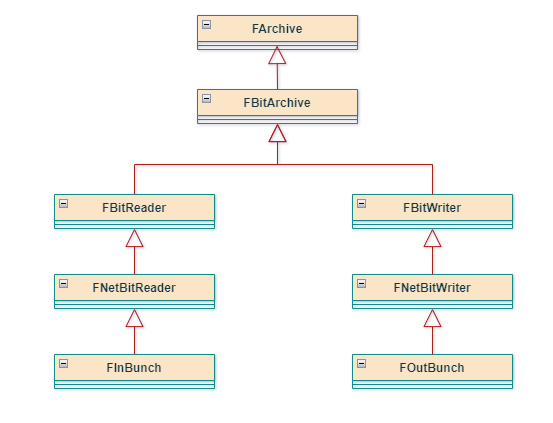
FInBunch 的结构如下:
class ENGINE_API FInBunch : public FNetBitReader | |
{ | |
public: | |
// 省略一些字段 | |
int32 PacketId; // Note this must stay as first member variable in FInBunch for FInBunch(FInBunch, bool) to work | |
FInBunch * Next; | |
UNetConnection * Connection; // 属于哪个 Connection | |
int32 ChIndex; // channel 的下标 | |
int32 ChType; // channel 的类型 | |
FName ChName; // channel 的名称 | |
int32 ChSequence; // Channel 的 Seqid | |
uint8 bOpen:1; // 是否是 Channel 的首包 | |
uint8 bClose:1; // 是否是 Channel 的结束包 | |
uint8 bDormant:1; // 是否处于休眠 | |
uint8 bIsReplicationPaused:1; // 复制同步是否被暂停了 | |
uint8 bReliable:1; // 是否为可靠的 Bunch | |
uint8 bPartial:1; // 该 Bunch 是否被拆分 | |
uint8 bPartialInitial:1; // 是不是分片传输中的第一个 Bunch | |
uint8 bPartialFinal:1; // 是不是分片传输中的最后一个 Bunch | |
} |
FOutBunch 的结构如下:
class ENGINE_API FOutBunch : public FNetBitWriter | |
{ | |
public: | |
// 省略一些字段 | |
FOutBunch * Next; | |
UChannel * Channel; | |
double Time; | |
int32 ChIndex; | |
int32 ChType; | |
FName ChName; | |
int32 ChSequence; | |
int32 PacketId; | |
uint8 ReceivedAck:1; // 标记这个数据包是否已经被确认,以避免重复发送 | |
uint8 bOpen:1; | |
uint8 bClose:1; | |
uint8 bDormant:1; | |
uint8 bReliable:1; | |
uint8 bPartial:1; // Not a complete bunch | |
uint8 bPartialInitial:1; // The first bunch of a partial bunch | |
uint8 bPartialFinal:1; // The final bunch of a partial bunch | |
} |
Bunch 的信息中,除了一些分包相关的信息,最主要的便是 Channel 相关的信息了,比如这个 Bunch 属于哪个 Channel?Channel 的类型是什么?那么什么是 Channel ?其用处是什么?
2.2 Channel 定义
UE 中,Channel 主要分为三种类型:
- ActorChannel: 用于在服务器和客户端之间同步Actor状态的通道。它负责在网络上移动、旋转、缩放等操作,并确保所有客户端都具有相同的Actor状态。它还负责同步Actor的变量和属性。
- ControlChannel:一个特殊类型的网络通道,主要负责处理底层的网络连接和控制消息。与其他类型的通道(如UActorChannel)主要用于游戏数据传输不同,UControlChannel处理的消息与游戏逻辑关系较少,主要用于维护网络连接状态、通知连接事件以及传输核心控制信息。ControlChannel 的一些职责示例如下:
- 连接建立和断开:UControlChannel会处理网络连接建立和断开的消息。例如,当客户端与服务器建立连接时,UControlChannel会发送和接收连接请求和响应,以便双方建立通信。同样,当连接断开时,UControlChannel会负责发送断开通知,通知另一方连接已关闭。
- 心跳检测:为了确保连接保持活跃,UControlChannel会定期发送和接收心跳消息。这些消息用于检测双方是否仍在线,以便在一方掉线时及时处理连接断开事件。
- 通道管理:UControlChannel负责处理通道的打开和关闭。例如,当需要创建一个新的UActorChannel以传输游戏对象数据时,UControlChannel会发送相应的打开通道请求。同样,当某个通道不再需要时,UControlChannel会负责发送关闭通道请求。
- 控制消息:UControlChannel还可以处理其他一些控制消息,如暂停、恢复游戏等。这些消息通常对游戏逻辑产生一定影响,但主要用于维护游戏状态和连接。
- VoiceChannel:主要处理语音数据,比如常见的游戏中的队伍聊天
2.3 Channel 的创建
-
Client :Client 上 Channel 的创建接口为
UNetDriver::CreateInitialCilentChannels,其实就是在 InitNetDriver 的时候就创建好了 Channel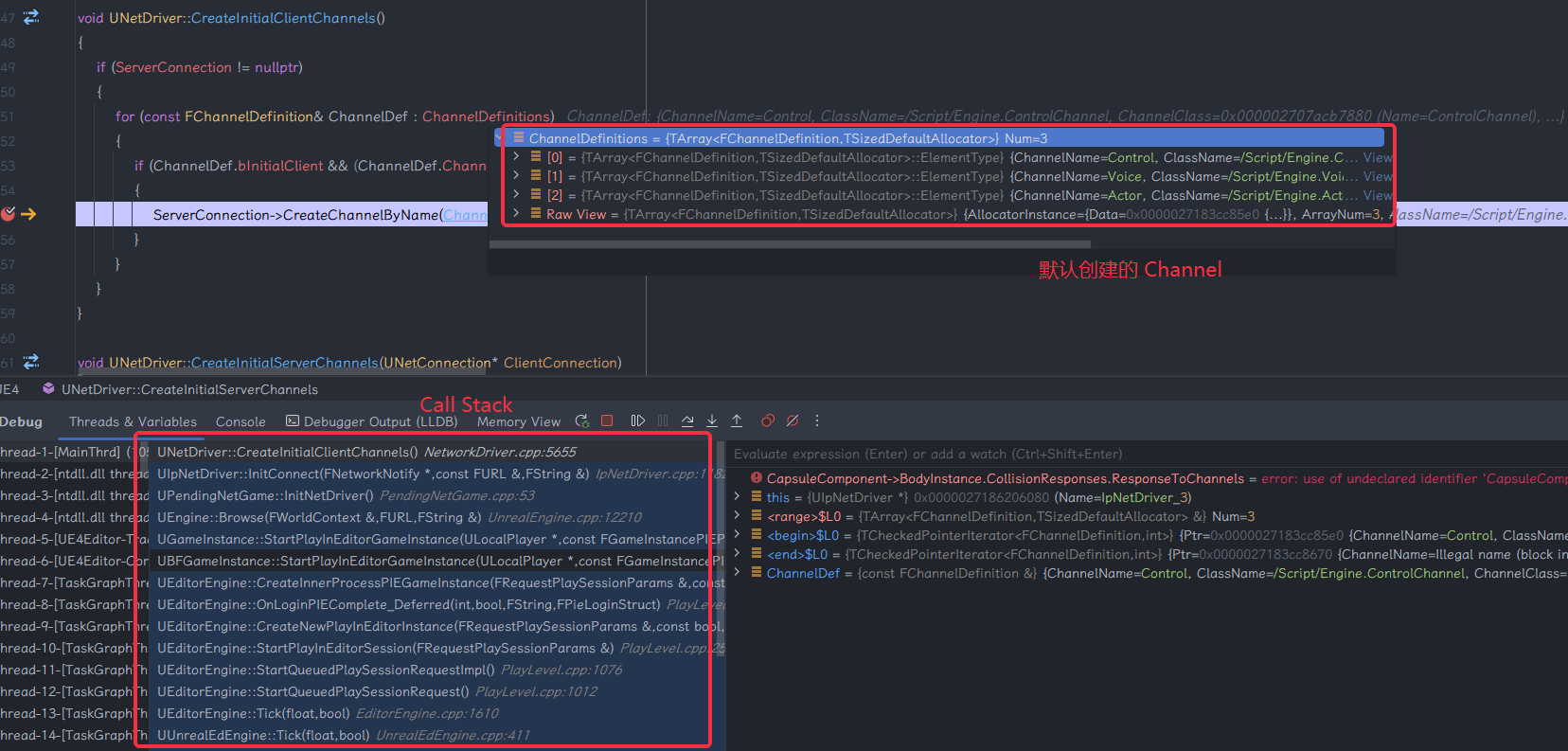
-
Server :Server 上 Channel 的创建时机如下:
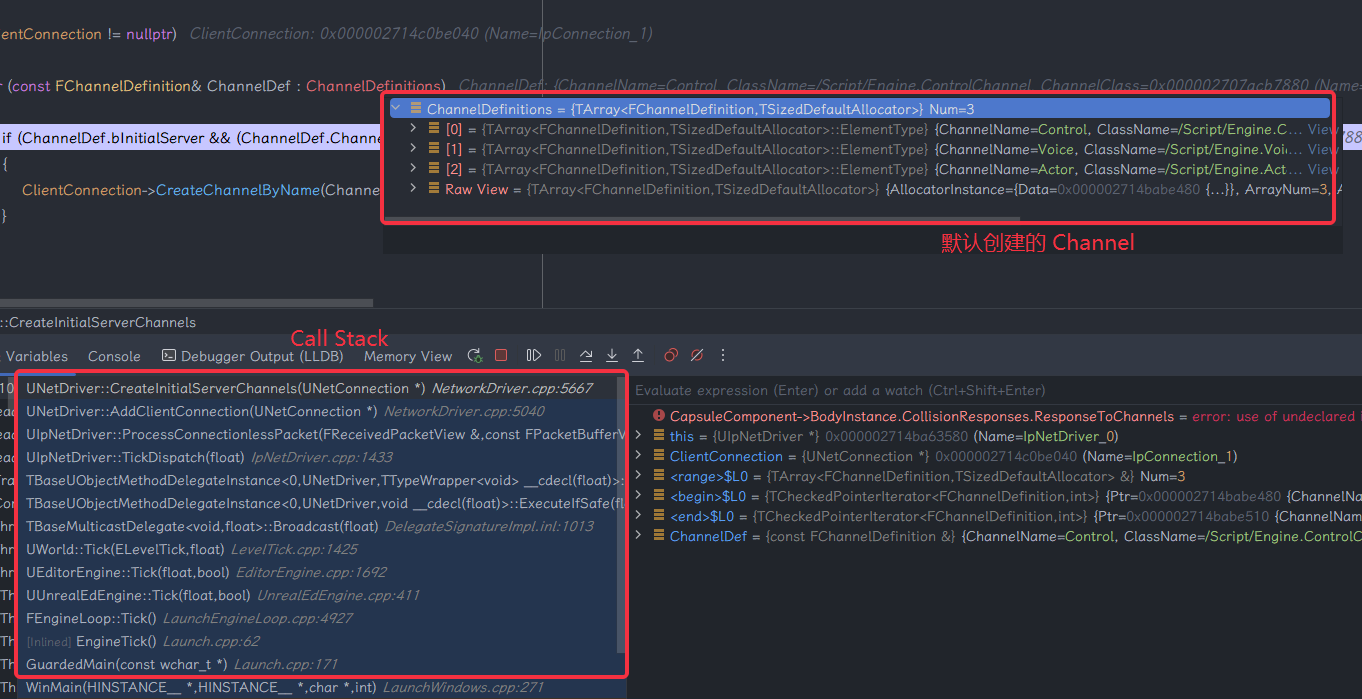
基本上都是在握手过程中就创建好了 Channel。其关系如下:

2.3 Client 发送 NMT_Hello
Server 端在 InitRemoteConnection 之后,会执行 UNetConnection::SetExpectedClientLoginMsgType(NMT_Hello) ,表示等待 Client 端发送 NMT_Hello 的消息,而 Client 端发送该消息的时机就在握手完毕之后。
Client 端在调用 BeginHandshake 的时候,会传入一个 Delegates,Handshake 完毕之后会调用 Delegates. Broadcast,通知握手完毕,绑定了该 Delegate 的接口都会被执行,大致如下:
// 握手完毕的回调 | |
void UPendingNetGame::InitNetDriver() { | |
// 省略一些代码 | |
// 发起握手,传入握手完毕的回调 | |
ServerConn->Handler->BeginHandshaking( FPacketHandlerHandshakeComplete::CreateUObject(this, &UPendingNetGame::SendInitialJoin)); | |
} | |
// SendInit | |
void UPendingNetGame::SendInitialJoin() { | |
// 省略一些代码 | |
// 发送 NMT_Hello | |
FNetControlMessage<NMT_Hello>::Send(ServerConn, IsLittleEndian, LocalNetworkVersion, EncryptionToken); | |
} |
因此握手完毕后,Client 端就会调用 UPendingNetGame::SendInitialJoin ,发送 NMT_Hello 给 Server 端。
这里还有个问题,如何确定这个 Message 会发送给 ControlChannel ?实际上这里由 FNetControlMessage<>::Send 接口处理,其内部实现会直接发送一个 FControlChannelOutBunch,该 Bunch 会直接使用 Channel[0] 初始化,Channel[0] 默认情况下就是 ControlChannel。
2.5 ControlChannel 处理 ControlMessage
2.5.1 Server
Server 端处理 Bunch 的 CallStack 如下:
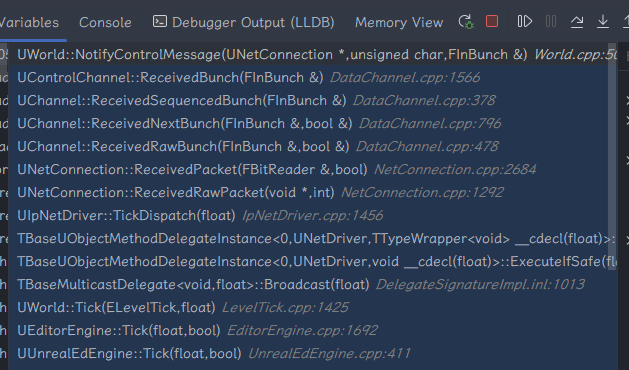
其大致流程如下:
- NetDriver 收到 Packet
- NetConnection 拆分 Packet 成多个 Bunch
- 根据 Bunch.ChIndex 找到对应的 Channel(Channel 缓存在 NetConnection)
- Channel 调用
ReceivedBunch(不同的 Channel 会各自重写该接口) - ControlChannel 收到 Message 后调用 NotifyControlMessage 进行广播,执行回调,其中 Server 登录流程相关的最主要的就是
UWorld::NotifyControlMessage接口
2.5.2 Client
Client 端登录过程中主要处理 ControlMessage 的接口为 UPendingNetGame::NotifyControlMessage
2.6 登录,加载地图,创建 PlayerController
- Server 端收到 NMT_Hello 后,会回复 NMT_Challenge
- Client 收到 NMT_Challenge 后,整合玩家数据 NickName,PlayerId 等,发送 NMT_Login
- Server 收到 NMT_Login:
- 设置 Connection 的 PlayerId
- 调用 GameMode::PreLogin,这里我们也可以定义自己的 PreLogin,来加一些 Token 校验之类的确定是否让玩家进入游戏。
- 返回 NMT_Welcome,同时会设置 LevelName,这样客户端就可以知道连接什么地图。
- Client 收到 NMT_Welcome:
- 设置地图路径,在 UPendingNetGame 的 URL 中,UEngine::TickWorldTravel 会一直轮询 UPendingNetGame 的地图 URL
- Travel 到目标地图
- 返回 NMT_NetSpeed 表示成功连接
- Server 收到 NMT_NetSpeed,没有什么特殊操作,只是简单设置下 NetSpeed
- Client 加载地图完毕,发送 NMT_Join。
UPendingNetGame::LoadMapCompleted->UPendingNetGame::SendJoin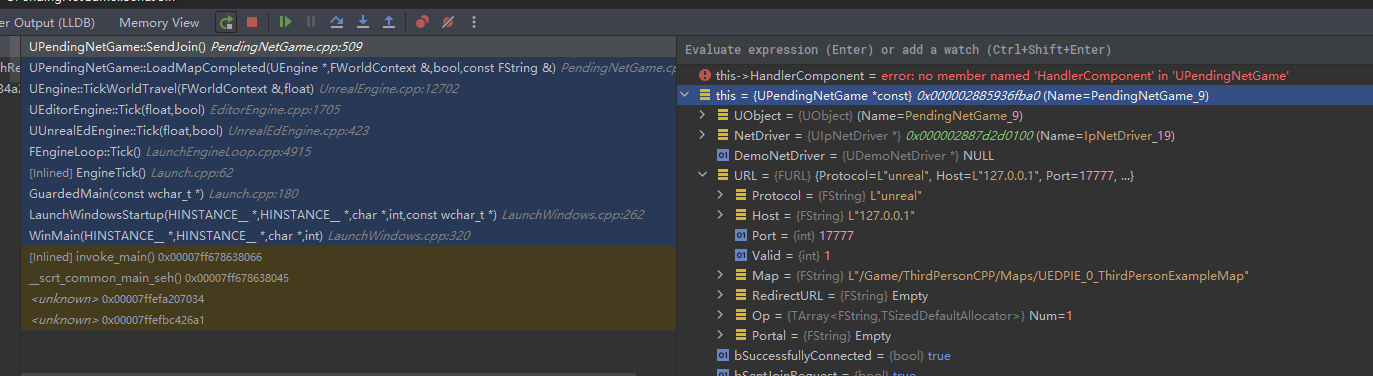
- Server 收到 NMT_Join:
- 如果对应的 Connection 没有 PlayerController 则创建一个
- 触发
AGameModeBase::Login - 如果当前 World 的 Map 是 Transition 的或者在一个错误的 World,则也通知 Client 再次进行 Travel
总体流程图如下: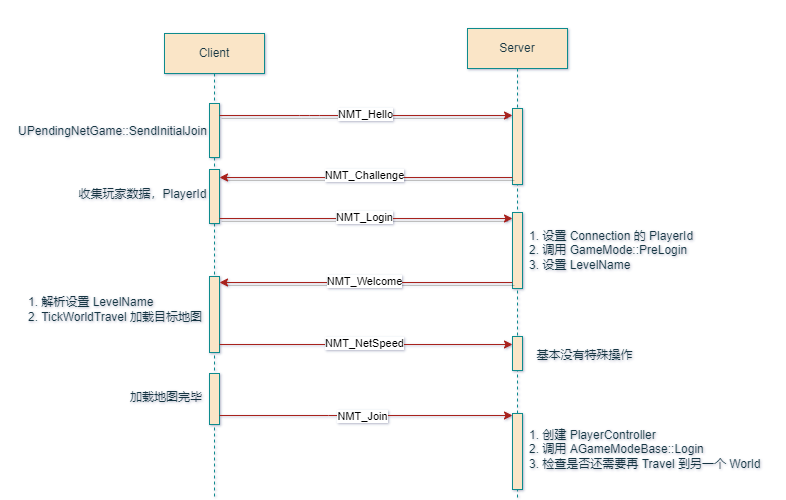
3. 总结
个人将 UE 中,Client 和 Server 建立连接到进入游戏中的过程分为了 2 步:
- 建立一个 UDP 连接(其实 UDP 没有连接的概念),并且在 Server 和 Client 都维护一个 UNetConnection
- 利用 Control Message 和 Control Channel 进行通信,进入游戏,执行 GameMode 的登录,加载地图,创建 PlayerController 等跟 Gameplay 密切相关的操作
